在二元高斯混合模型中求曲线积分
Jailbreaking 原理
对抗扰动矩阵分析
借用 FGSM 中的对抗样本生成方式,对抗扰动通过如下公式生成:
其中 是扰动的无穷范数约束条件 ,分析的重点是符号矩阵 。
假设该符号矩阵为实矩阵 。在黑盒设定下,关于该矩阵的假设几乎一无所知。
基于 MCMC 采样的文本生成
在受限文本生成 (Constrained Text Generation) 任务中,我们需要根据一些特定的信息 来生成目标文本 ,用数学的话说就是 。但是我们无法得到足够多的语料对 去直接监督一个条件语言模型,而只能训练一个无条件的语言模型 ,但是我们可以设计一个指标来定量的描述 和 之间的联系。
举例来说,用关键词造句,那么 就是关键词的集合,我们可以定义示性函数:
MCMC
马尔科夫链
在 马尔科夫及其有关的随机过程 中我们介绍过马尔科夫过程,其区别就是时间是否是离散的。整体分类可以见下面表格。
| 可数或�有限的状态空间 | 连续或一般的状态空间 | |
|---|---|---|
| 离散时间 | 在可数且有限状态空间下的马尔可夫链 | Harris chain (在一般状态空间下的马尔可夫链) |
| 连续时间 | Continuous-time Markov process | 任何具备马尔可夫性质的连续随机过程,例如维纳过程 |
Gumbel Softmax
之前已经写过 Reparameterization trick,这里主要是想重新讲讲整个重参数化的逻辑。
在 强化学习-基本组件 中说强化学习会将动作建模一个随机变量。即:
深度强化学习将会预测其动作的分布参数 ,然后在计算奖励函数时输入 ,但是问题是该 是从参数 下分布采样得到的。也就是说这个地方的梯度无法反传。
不可导函数的可导逼近
在深度学习中,我们会使用很多不可导函数,比如 ,,所以有一个很有意思的问题就是如何构造一个可导函数是的该函数逼近上述的不可导函数。当然该问题已经被大牛讨论很多次了 [^1][^2]
Max
我们想要寻找到一个平滑的二元函数 ,它的效果近似于 ��,足以用来代替最大值函数?在设计这样的函数时,下面这些条件需要尽可能满足:
强化学习 - 基本组件
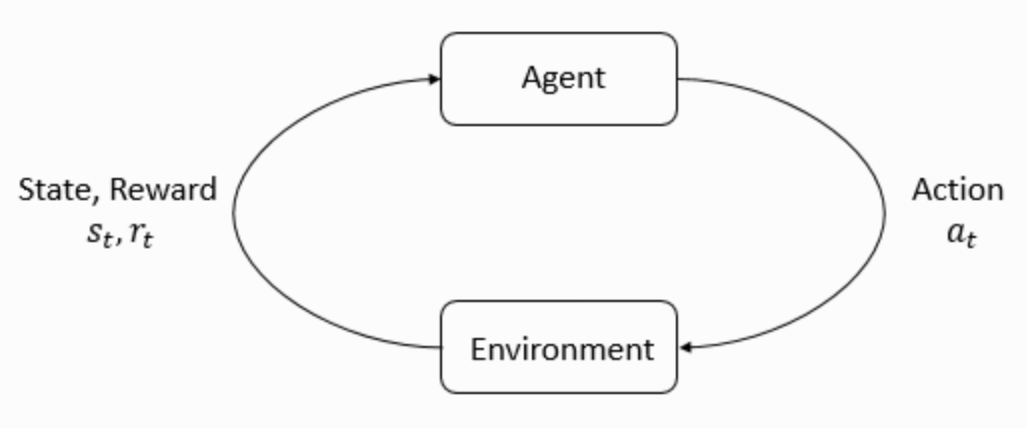
The main characters of RL are the agent and the environment. The environment is the world that the agent lives in and interacts with. At every step of interaction, the agent sees a (possibly partial) observation of the state of the world, and then decides on an action to take. The environment changes when the agent acts on it, but may also change on its own.
The agent also perceives a reward signal from the environment, a number that tells it how good or bad the current world state is. The goal of the agent is to maximize its cumulative reward, called return. Reinforcement learning methods are ways that the agent can learn behaviors to achieve its goal.
高斯过程
在 布朗运动与朗之万方程 中已经介绍过随机过程,而高斯过程 (Gaussian process) 是一个特殊的随机过程。在高斯过程中,连续输入空间中每个点都是与一个正态分布的随机变量相关联 [^1]。
从单变量高斯分布说起。在 单变量高斯分布 中我们已经写出了单变量高斯分布的公式,在这里重复一遍。
