Skip to main content

概率图

· 5 min read
PuQing
PuQing
AI, CVer, Pythoner, Half-stack Developer

概率图模型（Probabilistic Graphical Model， PGM），简称图模型（Graphical Model，GM），是指一种用图结构来描述多元随机变量之间条件独立性的概率模型，从而给研究高维空间的概率模型带来了很大的便捷性。

为什么讲条件独立性呢？

对于一个 KK 维随机向量，其联合概率为高维空间中的分布，一般难以直接建模。假设有

X=[X1,X2,⋯ ,XK]TX=\left[ X_{1},X_{2},\cdots,X_{K} \right]^{\mathbf{T}}

为离散随机变量并且有 mm 个取值，在不作任何假设的情况下，则需要 mK−1m^K-1 个参数才能表示其概率分布。参数是指数级的，我们在多元高斯分布中也反复说明过 高维问题，贝叶斯分类器条件假设。

一种可以减少参数量的方法就是独立性假设。将 KK 维随机变量的联合概率分解为 KK 个条件概率的乘积。

p(x)=P(X=x)=p(x1)p(x2∣x1)⋯p(xK∣x1,x2,⋯ ,xK−1)=∏k=1Kp(xk∣x1,⋯ ,xk−1)\begin{split} p(\mathbf{x})&=P(\mathbf{X}=\mathbf{x}) \\ & =p(x_{1})p(x_{2}\mid x_{1})\cdots p(x_{K}\mid x_{1},x_{2},\cdots,x_{K-1}) \\ & =\prod^{K}_{k=1}p(x_{k}\mid x_{1},\cdots,x_{k-1}) \end{split}

其中 xkx_{k} 表示变量 XkX_{k} 的取值。如果某些变量之间存在条件独立，其参数量就可以大幅减少。

info

假设有四个二值随机变量，在不知道这几个变量依赖关系的情况下，用一个联合概率表示需要 24−1=152^4-1=15 个参数。但是假设已知 X1X_{1} 时，X2X_{2} 和 X3X_{3} 独立，即有

p(x2∣x1,x3)=p(x2∣x1)p(x_{2}\mid x_{1},x_{3})=p(x_{2}\mid x_{1})

同理：p(x3∣x1,x2)=p(x3∣x1)p(x_{3}\mid x_{1},x_{2})=p(x_{3}\mid x_{1}) 当然，也可以写做：

p(x2,x3∣x1)=p(x2∣x1)p(x3∣x1)p(x_{2},x_{3}\mid x_{1}) = p(x_{2}\mid x_{1})p(x_{3}\mid x_{1})

另外，在已知 X2X_{2} 和 X3X_{3} 时，X1X_{1} 也和 X4X_{4} 独立，即有 p(x4∣x1,x2,x3)=p(x4∣x2,x3)p(x_{4}\mid x_{1},x_{2},x_{3})=p(x_{4}\mid x_{2},x_{3})

那么其联合概率 p(x)p(\mathbf{x}) 可以分解为：p(x)=p(x1)p(x2∣x1)p(x3∣x1)p(x4∣x2,x3)p(\mathbf{x})=p(x_{1})p(x_{2}\mid x_{1})p(x_{3}\mid x_{1})p(x_{4}\mid x_{2},x_{3})

这样就大大简化了联合概率分布的计算，而概率图可以直观的表示随机变量间条件独立性的关系。下面就是 44 个变量之间的条件独立性的图形化描述

Untitled.bmp

假设观测对象是高维随机变量 (x1,x2,⋯ ,xp)(x_{1},x_{2},\cdots,x_{p})，对于这样的高维随机变量而言，其概率满足一下规则

概率的规则​

基本运算法则
  1. Sum Rule\text{Sum Rule}：p(x1)=∫p(x1,x2) dx2p(x_{1})=\int p(x_{1},x_{2}) \, dx_{2} 就是求边缘概率
  2. Poduct Rule\text{Poduct Rule}：p(x1,x2)=p(x1∣x2)p(x2)=p(x2∣x1)p(x1)p(x_{1},x_{2})=p(x_{1}\mid x_{2})p(x_{2})=p(x_{2}\mid x_{1})p(x_{1})

根据这两个基本法则，可以推出下面法则：

tip
  1. Chain Rule\text{Chain Rule}：
p(x1,x2,⋯ ,xp)=p(x1)p(x2∣x1)p(x3∣x1,x2)…p(xn∣x1,x2,⋯ ,xn−1)=p(x1)∏j=2np(xj∣x1,x2,⋯ ,xj−1)\begin{split} \displaystyle p\left(x_{1}, x_{2}, \cdots, x_{p}\right)&=p(x_{1})p(x_{2}\mid x_{1})p(x_{3}\mid x_{1},x_{2})\dots p(x_{n}\mid x_{1},x_{2},\cdots,x_{n-1})\\ &=p(x_{1}) \prod^{n}_{j=2}p(x_{j}\mid x_{1},x_{2},\cdots,x_{j-1}) \end{split}
  1. Bayesian Rule\text{Bayesian Rule}
p(x2∣x1)=p(x1,x2)p(x1)=p(x1,x2)∫p(x1,x2)dx2=p(x2∣x1)p(x1)∫p(x2∣x1)p(x1)dx2p\left(x_{2} \mid x_{1}\right)=\frac{p\left(x_{1}, x_{2}\right)}{p\left(x_{1}\right)}=\frac{p\left(x_{1}, x_{2}\right)}{\int p\left(x_{1}, x_{2}\right) d x_{2}}=\frac{p\left(x_{2} \mid x_{1}\right) p\left(x_{1}\right)}{\int p\left(x_{2} \mid x_{1}\right) p\left(x_{1}\right) d x_{2}}

概述​

对于概率图模型我们有三个主要任务，表示、学习、推断

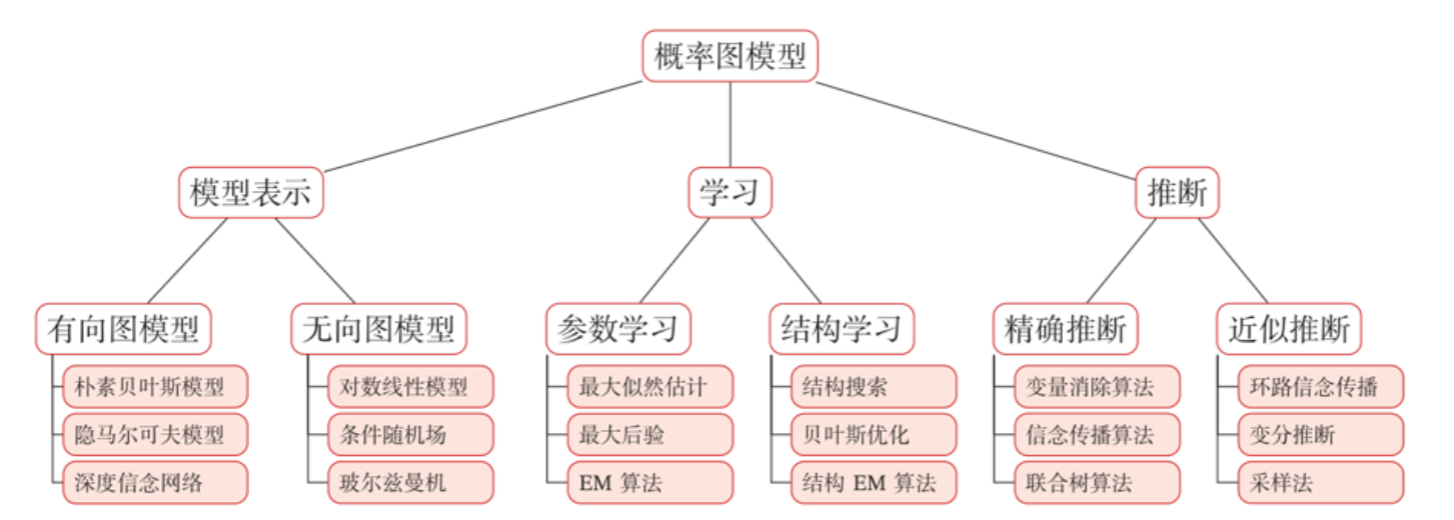
image.png

表示: 有向/无向​

  1. 有向图模型使用有向非循环图（Directed Acyclic Graph，DAG）来描述变量之间的关系。如果两个节点之间有连边，表示对应的两个变量为因果关系，即不存在其他变量使得这两个节点对应的变量条件独立。
info

有向图又称贝叶斯网络，从模型的条件独立性依赖的个数上看，可以分为单一模型和混合模型，单一模型条件依赖的集合就是单个元素，而混合模型条件依赖的集合则是多个元素。如果给模型加上时间概念，则可以有马尔科夫链和高斯过程等。从空间上，如果随机变量是连续的，则有如高斯贝叶斯网络这样的模型。混合模型加上时间序列，则有隐马尔科夫模型、卡尔曼滤波、粒子滤波等模型。

  1. 无向图模型使用无向图（Undirected Graph）来描述变量之间的关系。每条边代表两个变量之间有概率依赖关系，但是并不一定是因果关系。

相关资料​