Skip to main content

Koopman Theory

· 3 min read
PuQing
PuQing
AI, CVer, Pythoner, Half-stack Developer

Introduce​

Koopman 是使用线性系统用来近似非线性系统的一个符号算子，使用线性系统近似非线性系统后，就可以使用线性系统的控制理论来控制非线性系统了。

值得注意的是：

Koopman⁡\operatorname{Koopman} 算子是一个无穷维的线性变换，而我们要做的往往是用一个有限维度的 KK 矩阵去近似 Koopman⁡\operatorname{Koopman} 算子。而方法有：DMD、EDMD 和 Deep learning 的方法

线性系统​

在 仿射变换与仿射函数 中已经探讨过如何判断线性性。

即线性性具有 可加性，齐次性。对于线性系统来说：若该系统的微分方程满足线性性，则该系统为线性系统。

系统的线性是指对系统输入变量 rr 与输出变量 cc 的线性

例如函数：

c(t)=sin⁡(t)r(t)c(t) = \sin(t) r(t)

此时的 r(t)r(t) 才是输入，所以即便 sin⁡(t)\sin(t) 不是线性的，但是该系统仍然是线性的

warning

这里可能有点难以理解，我更想将这里的系统表述成某一种算子，它表示对于 信号 的一种 变换，这个跟前面一篇文章 Green 函数#Linear Differential Operators 是相通的，即：

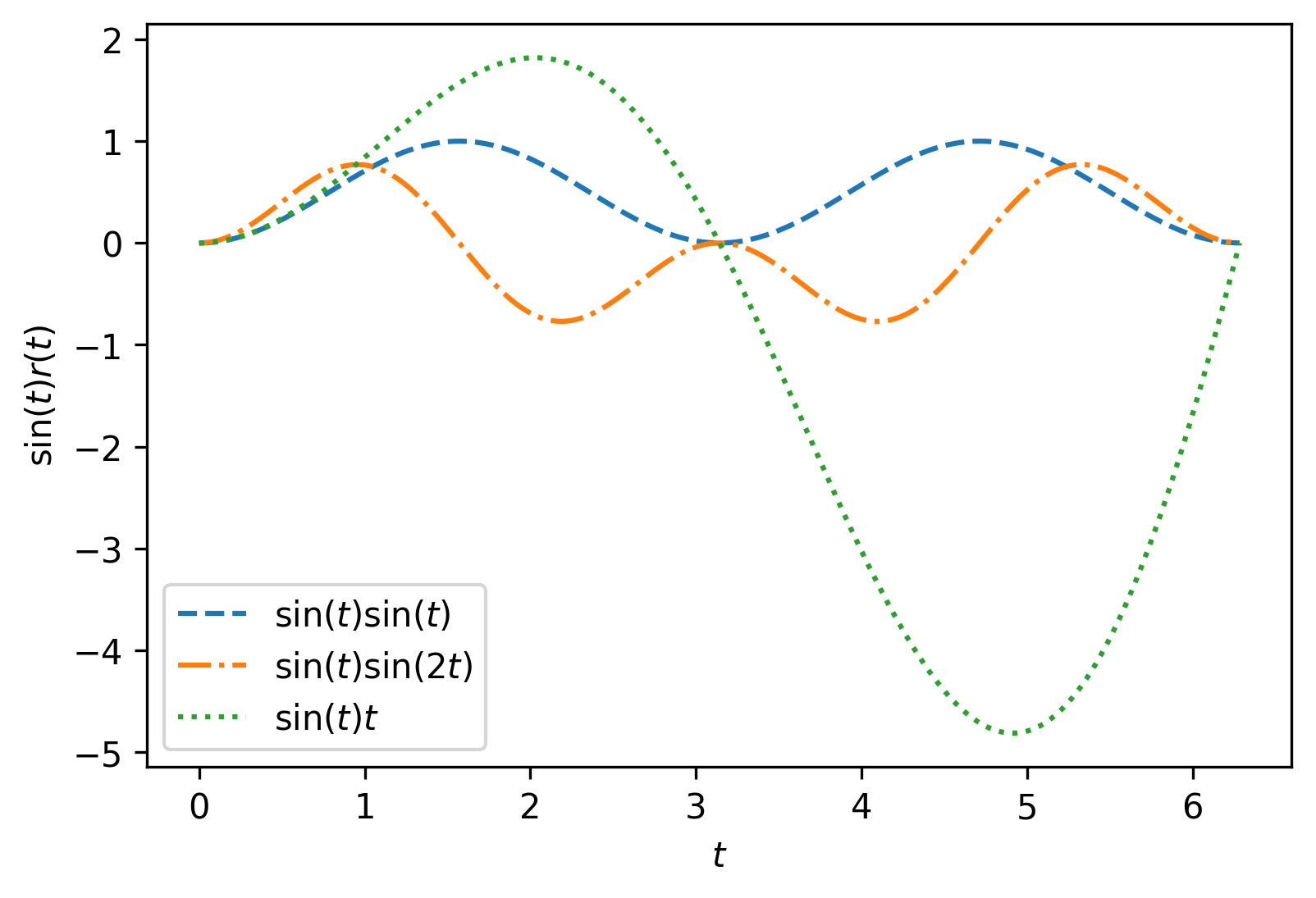
我们令 L=sin⁡(t)⋅L=\sin(t)\cdot，即算子 LL 就是 Element-wise 乘以 sin⁡(t)\sin(t)，下面我们将该 算子 作用到不同的 信号 上 image.png

这样的话，系统的线性性就很容易判断了，即我对输入 信号r(t)r(t)，做线性变换 kr(t)kr(t)，输出是否同步放缩 c(t)→kc(t)c(t)\to kc(t)，可加性 (叠加性) 同理。