∀x0∈I,x1=f(x0),x2=f(x1),x3=f(x2),…,xn=f(xn−1),…
则
∣x1−x2∣=∣f(x0)−f(x1)∣≤α∣x0−x1∣=α∣x0−f(x0)∣∣x2−x3∣=∣f(x1)−f(x2)∣≤α∣x1−x2∣=α2∣x0−f(x0)∣…∣xn−xn+1∣=∣f(xn−1)−f(xn)∣≤α∣xn−1−xn∣=αn−1∣x0−f(x0)∣从而
∣xn−xn+p∣≤∣xn−xn+1∣+∣xn+1−xn+2∣+…∣xn+p−1−xn+p∣≤(αn+αn+1+…+αn+p−1)∣x0−f(x0)∣≤1−ααn∣x0−f(x0)∣而由于 0<α<1,因此 {xn} 是 Cauchy 序列,设 limn→∞xn=x∗,x∗ 为 f(x) 在 I 上的不动点
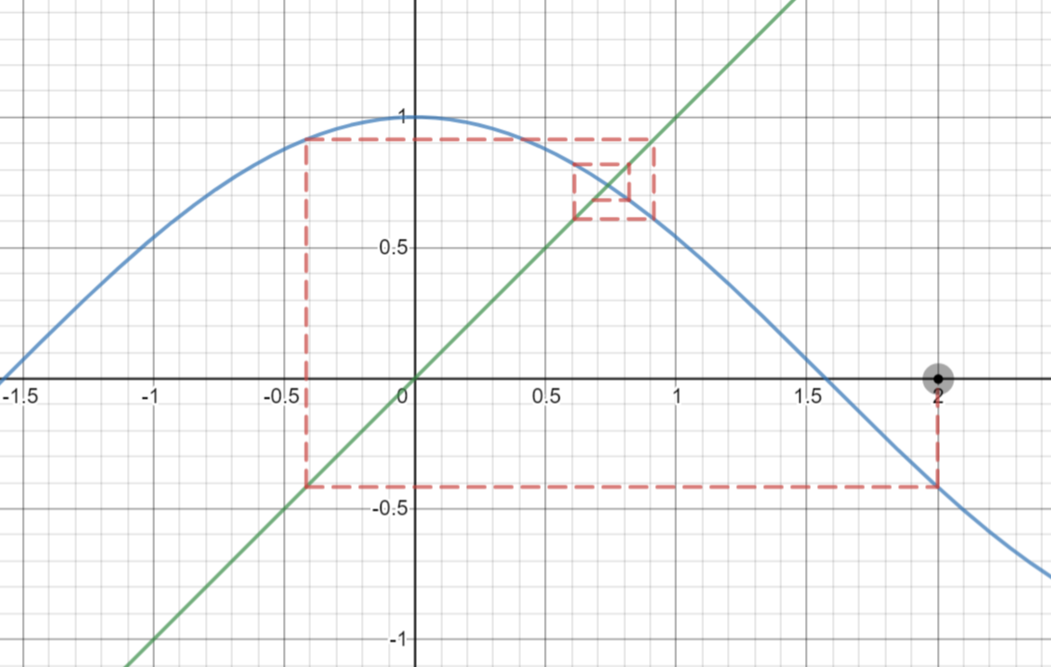 上面是其中的模拟;迭代的结果越来越逼近对角线 与余弦 的唯一交点。验算若干数值,不难作出如下猜想:不论实数的迭代序列
上面是其中的模拟;迭代的结果越来越逼近对角线 与余弦 的唯一交点。验算若干数值,不难作出如下猜想:不论实数的迭代序列