马尔科夫及其有关的随机过程

引言

在随机动力学中，马尔可夫 (Markov) 过程是一类特别重要的过程，这是因为：

1. 它能作为许多实际随机过程的模拟
2. 可应用已有的马尔可夫过程数学理论解决各种困难的随机问题
3. 它较易生成与模拟

以 $X(t)$ 表示马尔可夫过程。若过程 $X$ 之值与参数 $t$ 都是离散的，则称它为马尔可夫链。若 $X$ 之值连续，而 $t$ 是离散的，则称它为马尔可夫序列。这许多应用中，$X$ 之值与参数 $t$ 都是连续的，通常称之为马尔可夫过程。

马尔可夫过程

马尔可夫过程

若一个随机过程只有短暂记忆，现时状态只受最近历史的影响，这类过程统称为马尔可夫过程。一个随机过程 $X(t)$ 称为马尔可夫过程，若其条件概率满足

$$\begin{gather} \operatorname{Prob} \left[ X(t_{n}) \le x_{n} \mid X(t_{n-1}) \le x_{n-1},\cdots,X(t_{1})\le x_{1} \right] \\ = \operatorname{Prob}\left[ X(t_{n}) \le x_{n} \mid X(t_{n-1}) \le x_{n-1} \right] \tag{1} \end{gather}$$

式中 $t_{1}<t_{2}<\cdots<t_{n}$。显然，随机过程 $X(t)$ 为马尔可夫过程的充分条件是它在不重叠的两个时间区间上的增量独立。即若 $t_{1}<t_{2} \le t_{3}<t_{4}$，则 $\left[ X(t_{2})-X(t_{1})\right]$ 与 $\left[ X(t_{4})-X(t_{3}) \right]$ 独立。若 $X(t)$ 是高斯过程，则此充分条件为两个增量不相关，即

$$E\left\{ \left[ X(t_{2})-X(t_{1}) \right] \left[ X(t_{4})-X(t_{3}) \right] \right\} =0,\quad t_{1}<t_{2} \le t_{3} < t_{4} \tag{2}$$

显然，马尔可夫过程只是真实随机过程的数学理想化。但是，许多过程仍可用马尔可夫过程表示。物理中布朗运动是马尔可夫过程，各种领域如工程、通信、生态、生物中，许多噪声与信号过程常模型化为马尔可夫过程或借用马尔可夫过程。

对马尔可夫过程，定义 $(1)$ 可用下列概率密度函数表示：

$$p(x_{n},t_{n}\mid x_{n-1},t_{n-1};\cdots;x_{1},t_{1})=p(x_{n},t_{n}\mid x_{n-1},t_{n-1}) \tag{3}$$

利用 $(3)$ 与条件概率密度的性质，得

$$p(x_{1},t_{1};x_{2},t_{2};\cdots;x_{n},t_{n}) = p(x_{n},t_{n}\mid x_{n-1},t_{n-1})p(x_{n-1},t_{n-1}\mid x_{n-2},t_{n-2})\cdots p(x_{1},t_{1}) \tag{4}$$

推导

这个式子的推导很简单，不断的展开就行

$$\begin{aligned} p(x_{1},t_{1};x_{2},t_{2};\cdots;x_{n},t_{n})&=p(x_{n},t_{n}\mid x_{n-1},t_{n-1};\cdots;x_{2},t_{2};x_{1},t_{1}) p(x_{n-1},t_{n-1};\cdots,;x_{2},t_{2};x_{1},t_{1}) \\ &=p(x_{n},t_{n}\mid x_{n-1},t_{n-1}) p(x_{n-1},t_{n-1};\cdots,;x_{2},t_{2};x_{1},t_{1}) \\ & \dots \\ & = p(x_{n},t_{n}\mid x_{n-1},t_{n-1})p(x_{n-1},t_{n-1}\mid x_{n-2},t_{n-2}) \cdots p(x_{1},t_{1}) \end{aligned}$$

方程 $(4)$ 表明，高阶概率密度可从初始概率密度与条件概率密度得到。换而言之，马尔可夫过程完全由其条件概率密度与初始概率密度表征。后者包括初始状态为固定，即初始概率密度为狄拉克 $\delta$ 函数之情形。因此，为量化马尔可夫过程 $X(t)$，条件概率密度 $p(x_{k},t_{k}\mid x_{j},t_{j})$ 是最重要的。条件概率密度又称转移概率密度。若其转移概率密度不随时间平移而改变，则称该马尔可夫过程为平稳，即对任一时间平移 $\Delta t$，

$$p(x_{k},t_{k}\mid x_{j},t_{j}) = p(x_{k},t_{k}+\Delta t\mid x_{j},t_{j}+\Delta t)=p(x_{\tau},\tau\mid x_{0},0) \tag{5}$$

其中 $\tau=t_{k}-t_{j}$，$x_{\tau}$ 和 $x_{0}$ 分别是 $X(\tau)$ 和 $X(0)$ 的状态变量。此时，平稳概率密度可令转移时间区间趋于无穷得到，即

$$p(x) = \lim_{ \tau \to \infty } p(x,\tau\mid x_{0}) \tag{6}$$

这个地方不是太理解

上述标量马尔可夫过程的概率易推广于矢量马尔可夫过程。设 $\boldsymbol{X}(t)=\left[ X_{1}(t),X_{2}(t),\cdots,X_{n}(t) \right]^{\mathsf{T}}$ 为 $n$ 维矢量马尔可夫过程，它满足

$$p(\boldsymbol{x}_{n},t_{n}\mid \boldsymbol{x}_{n-1},t_{n-1};\cdots;\boldsymbol{x}_{1},t_{1}) = p(\boldsymbol{x}_{n},t_{n}\mid \boldsymbol{x}_{n-1},t_{n-1}) \tag{7}$$

注意，矢量马尔可夫过程的分量可以是也可以不是标量马尔可夫过程。

福克 - 普朗克 - 柯尔莫哥洛夫方程

考虑三个时刻 $t_{1}<t<t_{2}$，由 $(7)$ 与 $(4)$ 可得

$$p(x_{2},t_{2}\mid \boldsymbol{y},t;x_{1},t_{1})=p(x_{2},t_{2}\mid \boldsymbol{y},t)p(\boldsymbol{y},t\mid x_{1},t_{1}) \tag{8}$$

该式子表达的意思

这个地方如果是从马尔可夫链进行推导，即离散形式的条件概率可能会更直观。

在前面的推导我们知道式 $(3)$，可是我们如何知道下下个时刻的条件概率呢？

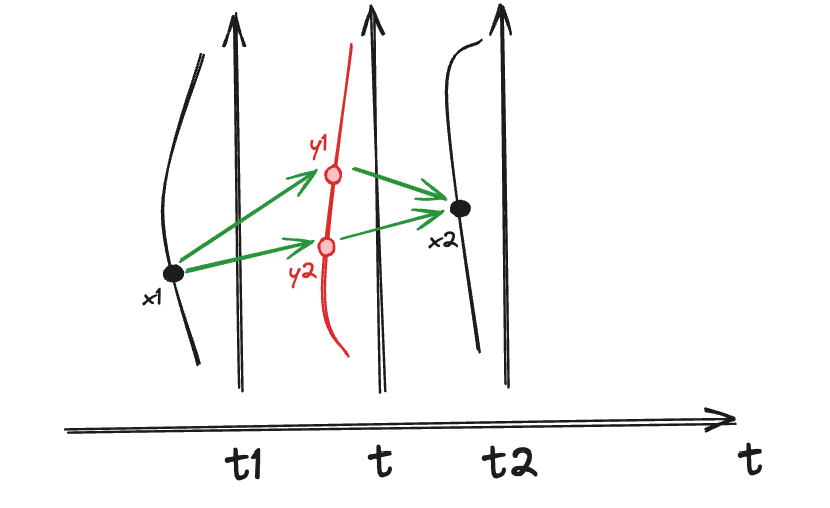
在式 $(8)$ 就是假设，$t_{1}$ 通过 $y$ 转移到 $t_{2}$ 上，但是 $y$ 是不固定的，所以下面要取积分

在 $(8)$ 中对 $y$ 积分，得

$$p(x_{2},t_{2}\mid x_{1},t_{1})=\int p(x_{2},t_{2}\mid \boldsymbol{y},t)p(\boldsymbol{y},t\mid x_{1},t_{1})\, d \boldsymbol{y} \tag{9}$$

式 $(9)$ 就是著名的查普曼 - 柯尔莫哥洛夫 - 斯莫拉伍斯基 (Chapman-Kolmogorov-Smoluwski) 方程，它是支配转移概率密度的积分方程。为了便于分析，积分方程 $(9)$ 可转化为等价的微分方程，即著名的福克 - 普朗克 - 柯尔莫哥洛夫 (Fokker-Planck-Kolmogorov, FPK) 方程

$$\frac{\partial}{\partial t}p + \sum^{n}_{j=1} \frac{\partial}{\partial x_{j}}(a_{j}p)-\frac{1}{2} \sum_{j,k=1}^n \frac{ \partial^{2}}{ \partial x_{j} \partial x_{k} } (b_{jk}p) + \frac{1}{3!} \sum_{j,k,l=1}^n \frac{ \partial^{3}}{ \partial x_{j} \partial x_{k} \partial x_{l}}(c_{jkl}p)-\cdots=0 \tag{10}$$

式中 $p=p(x,t\mid x_{0},t_{0})$ 是转移概率密度，

$$\begin{equation} \begin{split} &a_{j}=a_{j}(\boldsymbol{x}, t)=\lim _{\Delta t \rightarrow 0} \frac{1}{\Delta t} E\left[X_{j}(t+\Delta t)-X_{j}(t) \mid \boldsymbol{X}(t)=\boldsymbol{x}\right], \\ &b_{j k}=b_{j k}(\boldsymbol{x}, t)=\lim _{\Delta t \rightarrow 0} \frac{1}{\Delta t} E\left\{\left[X_{j}(t+\Delta t)-X_{j}(t)\right]\left[X_{k}(t+\Delta t)-X_{k}(t)\right] \mid \boldsymbol{X}(t)=\boldsymbol{x}\right\}, \\ & c_{j k l}=c_{j k l}(\boldsymbol{x}, t)=\lim _{\Delta t \rightarrow 0} \frac{1}{\Delta t} E\left\{\left[X_{j}(t+\Delta t)-X_{j}(t)\right]\left[X_{k}(t+\Delta t)-X_{k}(t)\right]\right. \\ & \quad \qquad \qquad \qquad \left.\times\left[X_{l}(t+\Delta t)-X_{l}(t)\right] \mid \boldsymbol{X}(t)=\boldsymbol{x}\right\}, \\ & \cdots \end{split} \end{equation} \tag{11}$$

函数 $a_{j},b_{jk},c_{jkl},\cdots$ 称为导数矩，它给出在 $X(t)=x$ 条件下，在 $t$ 时刻上 $X(t)$ 的各增量矩的速率。

在许多实际问题中，高于二阶的导数矩为零，于是 $(10)$ 化为

$$\frac{\partial}{\partial t} p+\sum_{j=1}^{n} \frac{\partial}{\partial x_{j}}\left(a_{j} p\right)-\frac{1}{2} \sum_{j, k=1}^{n} \frac{\partial^{2}}{\partial x_{j} \partial x_{k}}\left(b_{j k} p\right)=0 . \tag{12}$$

通常所说的 FPK 方程是指 $(12)$，此时，马尔可夫过程 $X(t)$ 称为马尔可夫扩散过程，或简称扩散过程。

FPK 方程 $(12)$ 可重写为

$$\frac{\partial}{\partial t}p + \sum_{j=1}^{n} \frac{\partial}{\partial x_{j}}G_{j}=0, \tag{13}$$

式中

$$G_{j} = a_{j}p - \frac{1}{2} \sum^{n}_{k=1} \frac{\partial}{\partial x_{k}}(b_{jk}p). \tag{14}$$