仿射变换与仿射函数

仿射变换

仿射变换 (Affine transformation)，又称为仿射映射，是指在几何中，对一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间 ¹

有向量 $\vec{x}$，以及有线性变换矩阵 $\mathbf{A}$，以及平移向量 $\mathbf{b}$。则有仿射变换：

$$\vec{y} = \mathbf{A}\vec{x}+\mathbf{b}$$

假设该映射是一个 $\mathbb{R}^n \to \mathbb{R}^m$ 的映射，则其中的矩阵 $\mathbf{A}$ 是一个 $m\times n$ 的矩阵，$\mathbf{b}$ 是一个 $m$ 维向量。

仿射函数

若上面的映射是一个 $\mathbb{R}^n \to \mathbb{R}$ 的映射，则我们称 $y=Ax+b$ 是一个仿射函数，形如：

$$y = \begin{bmatrix} a_1 & \cdots & a_n \end{bmatrix}\times \begin{bmatrix} x_1 \\ \vdots \\ x_n \end{bmatrix} + b$$

性质

仿射变换保留了：

tip

1. 点之间的 共线性：在同一条直线上的三个或更多的点（称为共线点）在变换后依然在同一条直线上（共线）；
2. 直线的 平行性：两条或以上的平行直线，在变换后依然平行；
3. 集合的 凸性：凸集合变换后依然是凸集合。并且，最初的 极值点 被映射到变换后的极值点集；
4. 平行线段的长度的比例：两条由点 $p_{1},p_{2},p_{3},p_{4}$ 定义的平行线段，$\overrightarrow{p_{1} p_{2}}$ 与 $\overrightarrow{p_{3} p_{4}}$ 的长度的比例等于 $\overrightarrow{f\left(p_{1}\right) f\left(p_{2}\right)}$ 与 $\overrightarrow{f\left(p_{3}\right) f\left(p_{4}\right)}$ 的长度的比例；

仿射变换为 可逆 当且仅当 $\mathbf{A}$ 为可逆的。

性质

如果函数 $f:\mathbb{R}^n \to \mathbb{R}^m$ 是仿射映射，对于任意的 $x,y \in \mathbb{R}^n, \alpha,\beta\in \mathbb{R}$ 且 $\alpha+\beta=1$，存在

$$f(\alpha x+\beta y)=\alpha f(x)+\beta f(y)$$

这里突然要求 $\alpha+\beta=1$，我觉得不太自然。

关于 $\alpha+\beta=1$ 的解释

我们知道线性系统是具有 可加性，齐次性 的，即

$$\begin{align} \text{可加性} L(\vec{v}+\vec{w}) & = L(\vec{v})+L(\vec{w})\\ \text{齐次性} L(n \vec{v}) & = n L(\vec{v}) \end{align}$$

可是对于平移运算并不满足上述两个性质

$$\begin{align} \underbrace{(v+w)+b}_{f(v+w)} \ne \underbrace{v+b}_{f(v)} +\underbrace{w+b}_{f(w)} \end{align}$$$$\begin{align} \underbrace{\alpha x+b}_{f(\alpha x)} \ne \underbrace{\alpha (x+b)}_{\alpha f(x)} \end{align}$$

所以要求对输入组合进行加权，而权和为 1

$$\begin{align} \underbrace{\alpha v+\beta w +b}_{f(\alpha v+\beta w)} =\underbrace{\alpha (v+b)}_{\alpha (f(v))} +\underbrace{\beta (w+b)}_{\beta f(w)} =\alpha v+\beta w+({\color{Red} \alpha +\beta } )b \end{align}$$

^beaa3f

线性和仿射变换的区别

可能有地方将类似于 $y=kx+b$ 的式子也称为线性函数，可是从上面可知，该式子称其是仿射函数更为准确，而严格的线性应为 $y=kx$。

而区别是过原点与否的区别：

应用

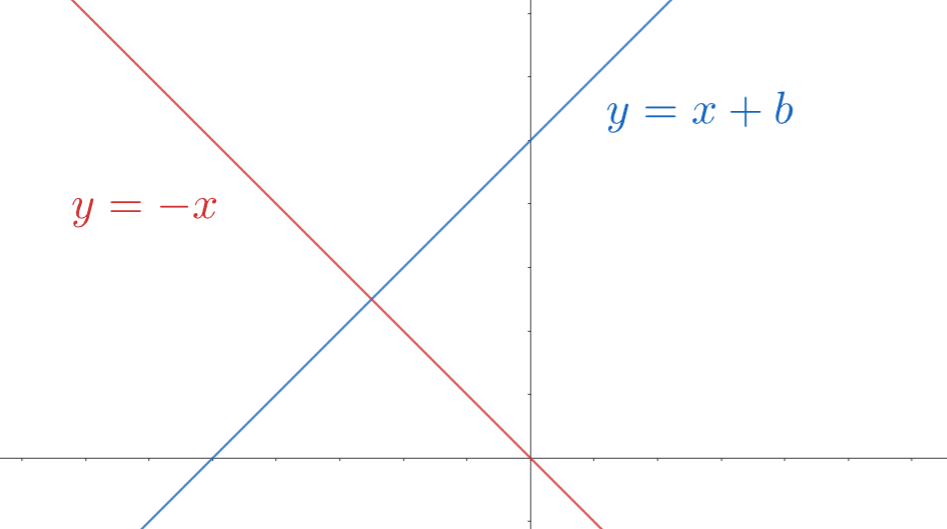
在 MindFlow 实习中曾经看到过对于 单纯形的采样，即在 $\mathbb{R}^2$ 上的三角形皆可以由仿射变换来达成，所有的平行四边形也可以，但是一般四边形不可以。

可以构建一个仿射变换，使得可以转换。

我们的目的是寻找这样的一个映射，使得左边可以转换到右边，即：

$$\left[\begin{array}{l} x \\ y \end{array}\right] \mapsto \mathbf{A}\left[\begin{array}{l} x \\ y \end{array}\right]+b$$

显然，先讨论平移量更为方便，即为变换后三角形中任意一点坐标，这里取 $(x_{1},y_{1})$

然后变基，将基向量转换为三角形两条边。

即：

$$\begin{bmatrix} x_2-x_1 & x_3-x_1 \\ y_2-y_1 & y_3-y_1 \end{bmatrix}$$

于是可得到仿射映射：

$$\left[\begin{array}{l} x \\ y \end{array}\right] \mapsto \begin{bmatrix} x_2-x_1 & x_3-x_1 \\ y_2-y_1 & y_3-y_1 \end{bmatrix}\left[\begin{array}{l} x \\ y \end{array}\right]+\begin{bmatrix} x_1 \\ x_1 \end{bmatrix}$$

Footnotes

1. 仿射变换 - 维基百科，自由的百科全书 ↩