Word Embedding

September 4, 2023 · 3 min read

AI, CVer, Pythoner, Half-stack Developer

info

在谈到 Embedding 不得不谈到 Word Embedding

单词的表达

类似于图像分类任务中的 One Hot 编码，我们可以对于单词施行 One Hot Representation.

实例

有 1000 个词汇量。排在第一个位置的代表英语中的冠词 “a”，那么这个 “a” 是用 $[1,0,0,0,0,\dots]$ ，只有第一个位置是 1，其余位置都是 0 的 1000 维度的向量表示，如下图中的第一列所示。

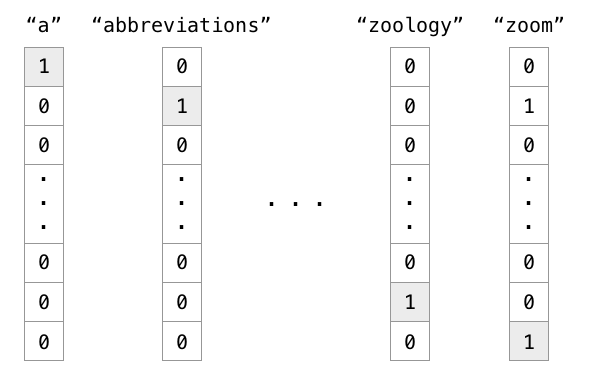
也就是说，

info

One Hot 编码的每个单词就是一个维度，每个单词之间是 independent 的

但是上面的编码方式很稀疏，丧失了单词之间的联系，有没有一种编码方式能够隐式的嵌入单词之间的关系？

考虑这样的表格：

		0	1
0	gender	female	male
1	age	child	adult

这个表格中的 $gender$ , $age$ 可以视为 “ 特征 “，而 $0,1,\dots$ 则是该特征的特征值

我们手动寻求这四个单词之间的关系 $f$ ，然后可以使用在两个特征上的值去表示四个单词

info

\begin{cases} female \mapsto [0,0]\\ child \mapsto [1,0] \\ \cdots \end{cases}

但是就如图像处理中的各种 $\mathrm{kernel}$ 一样（如， $\mathrm{Sobel,Canny,\dots}$ ），我们在 $\mathrm{CNN}$ 中采用了卷积核用来自动 ” 提取特征 “；是不是我们可以在这里采用同样的思路。

info

Word Embedding 就是要从数据中自动学习到输入空间到 Distributed representation 空间的映射 $f$

那一个非常粗暴的方式是什么呢，我直接学一个矩阵，假设输入词汇量 $N$ ，想要提取出 $M$ 个特征，那我学一个 $N\times M$ 的转换矩阵就好。

\begin{bmatrix} a_1 \\ a_2 \\ \cdots \\ a_{n-1}\\ a_n \end{bmatrix}\times \begin{bmatrix} w_{1.1} & w_{1.2} & \cdots & w_{1.n-1} & w_{1.n}\\ & & \vdots \\ & &\vdots\\ & &\vdots\\ w_{m} & w_{m}& \cdots & w_{m.n-1} & w_{m.n} \end{bmatrix}= \begin{bmatrix} b_1 \\ b_2 \\ \cdots \\ b_{m-1}\\ b_m \end{bmatrix}

我们预先是不可能知道这个转换矩阵是怎么样的，下面有两种方法。

从各个输入 $\left\{x_{i}{ }_{i=1}^{N}\right\}$ 之间的关系找目标。如聚类
接下游任务。我们的 Embedding 网络就是需要学习 $x\mapsto y$ ，那我们给定数据 $\left\{\left(x_{i}, z_{i}\right)_{i=1}^{N}\right\}$ ，我们可以去学习一个 $x\mapsto z$ ，这个网络由两个部分构成 $x\mapsto y$ ，以及 $y\mapsto z$ ，于是等到网络训练完毕，则自然学到了映射 $x\mapsto y$

tip

这里类比图像中的各个任务，Embedding 层就类似于 Backbone，而文字的下游任务可以是单词情感等 (几种不同的任务)

像啊，很像啊

上面说到的后两种任务，有很熟悉的味道。何凯明大佬的 $\mathrm{MAE}$ ¹，与这个是什么关系，似乎叫掩码自编码