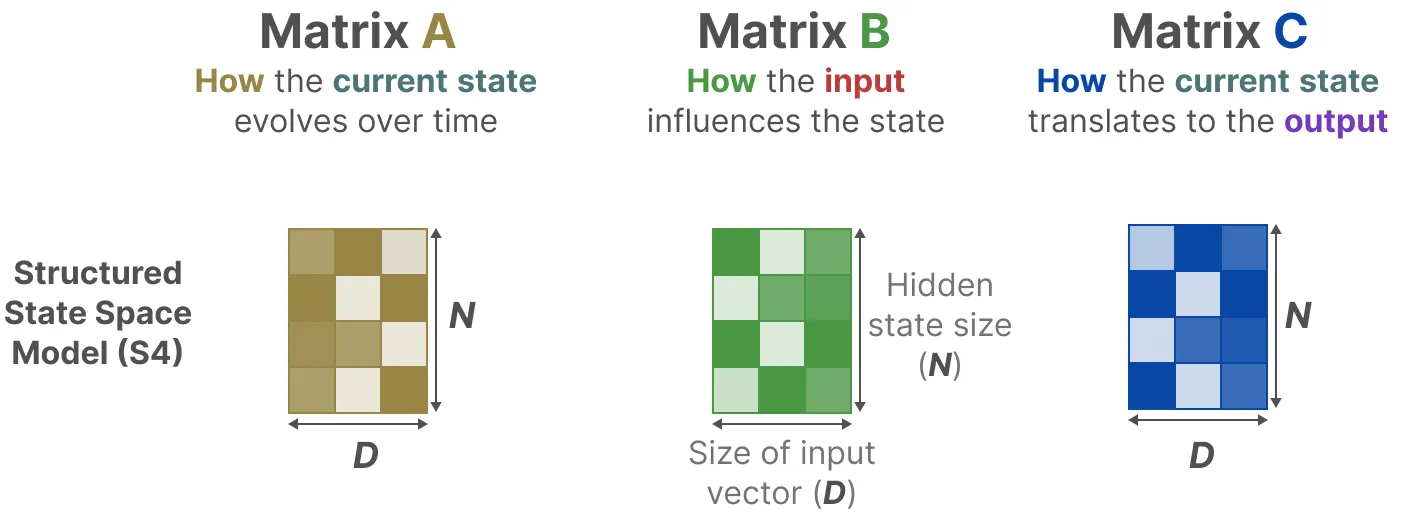
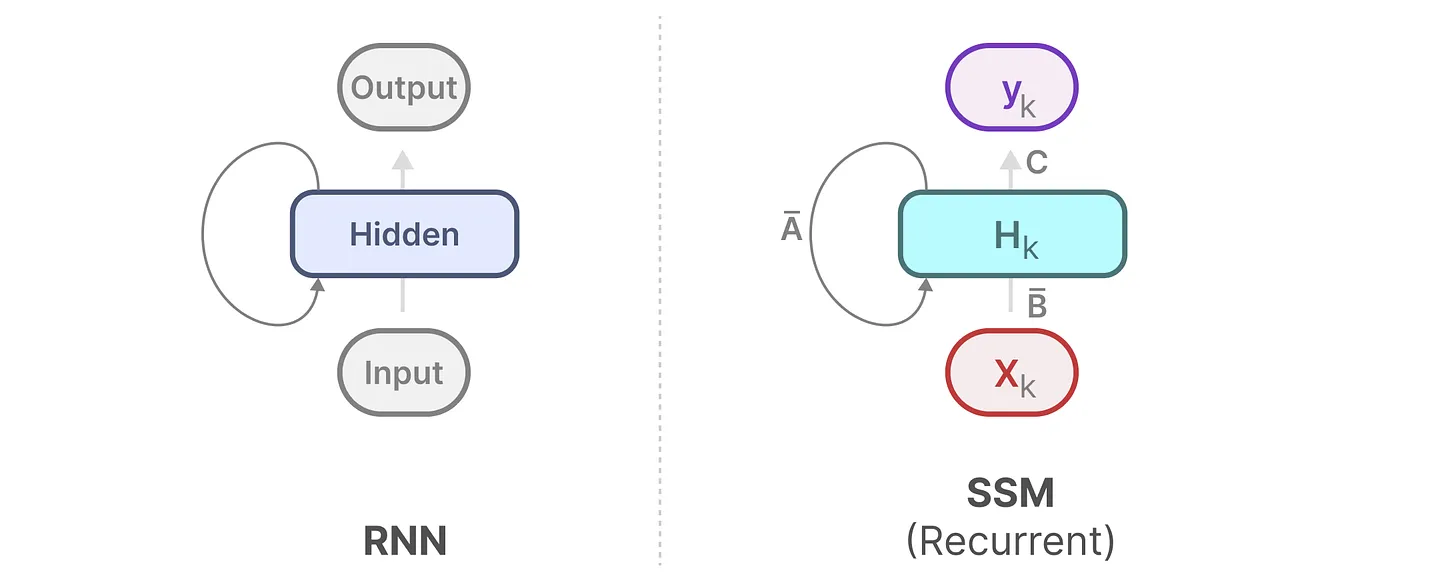
什么是 SSM
状态空间模型(State Space Models,SSM),与 线性系统入门-动态系统 中我们介绍过线性时不变系统就是一个东西。
{ d x ( t ) d t = A x ( t ) + B u ( t ) ∈ R N y ( t ) = C x ( t ) + D u ( t ) ∈ R \begin{cases}
\displaystyle \frac{d \boldsymbol{x}(t)}{d t}=\boldsymbol{A} \boldsymbol{x}(t)+\boldsymbol{B} u(t) \in \mathbb{R}^{N} \\
y(t)=\boldsymbol{C} \boldsymbol{x}(t)+\boldsymbol{D} u(t) \in \mathbb{R}
\end{cases} ⎩ ⎨ ⎧ d t d x ( t ) = A x ( t ) + B u ( t ) ∈ R N y ( t ) = C x ( t ) + D u ( t ) ∈ R 其中每个矩阵是具有含义的,其中的 A \boldsymbol{A} A B \boldsymbol{B} B C \boldsymbol{C} C D \boldsymbol{D} D
HiPPO(High-order Polynomial Projection Operators)
HiPPO1 遗忘问题
fixed-size context windows:Transformer 的 window size 通常是有限的,一般来说 Quadratic 的 Attention 最多建模到大约 10K 的 Token 就到计算极限了
vanishing gradient:RNN 通过 hidden state 来存储历史信息,理论上能记住之前所有内容,但是实际上 effective memory 大概是 < 1 K <1K < 1 K
在线函数逼近(Online Function Approximation)
问题的设定是:
考虑一个一维函数,我们能否用一个固定大小的 representation c ( t ) ∈ R N c(t) \in \mathbb{R}^N c ( t ) ∈ R N f f f [ 0 , t ] [0,t] [ 0 , t ] f ≤ t f_{\leq t} f ≤ t t t t t 1 t_{1} t 1 t 2 t_{2} t 2 c ( t 1 ) c(t_{1}) c ( t 1 ) c ( t 2 ) c(t_{2}) c ( t 2 ) f ≤ t 2 f_{\leq t_{2}} f ≤ t 2
为了判断拟合的效果,我们需要一个测度 (measure) 来判定拟合出来的连续函数和原来的连续函数的相似度,并且假设对于不同的 time step x x x μ ( x ) \mu(x) μ ( x )
⟨ f , g ⟩ μ = ∫ 0 ∞ f ( x ) g ( x ) d μ ( x ) \langle f, g\rangle_{\mu}=\int_{0}^{\infty} f(x) g(x) \mathrm{d} \mu(x) ⟨ f , g ⟩ μ = ∫ 0 ∞ f ( x ) g ( x ) d μ ( x ) 如何用
N N N 维向量来 encoder
f ≤ t f_{\leq t} f ≤ t 假设一组多项式正交基 G = { g n } n < N \mathcal{G}=\{g_{n}\}_{n<N} G = { g n } n < N ⟨ g i , g j ⟩ μ = 0 \langle g_{i}, g_{j}\rangle_{\mu}=0 ⟨ g i , g j ⟩ μ = 0 μ \mu μ μ \mu μ G \mathcal{G} G f ≤ t f_{\leq t} f ≤ t G \mathcal{G} G c ( t ) c(t) c ( t )
c n ( t ) : = ⟨ f ≤ t , g n ⟩ μ ( t ) c_{n}^{(t)}:=\left\langle f_{\leq t}, g_{n}\right\rangle_{\mu^{(t)}} c n ( t ) := ⟨ f ≤ t , g n ⟩ μ ( t ) 也就是说 c ( t ) c(t) c ( t ) c n c_{n} c n
从离散的角度来理解的话,从 t = 0 t=0 t = 0 f ( t ) f(t) f ( t ) c ( t ) c(t) c ( t ) f ≤ t f_{\leq t} f ≤ t f ( t + 1 ) f(t+1) f ( t + 1 ) c ( t + 1 ) c(t+1) c ( t + 1 ) f ≤ t + 1 f_{\leq t+1} f ≤ t + 1 c ( t + 1 ) c(t+1) c ( t + 1 ) c ( t ) c(t) c ( t ) f ( t + 1 ) f(t+1) f ( t + 1 )
c ˙ ( t ) = A ( t ) c ( t ) + B ( t ) f ( t ) \dot{c}(t) = A(t)c(t)+B(t)f(t) c ˙ ( t ) = A ( t ) c ( t ) + B ( t ) f ( t ) 只要给定 measure μ \mu μ A ∈ R N × N , B ∈ R N × 1 A \in \mathbb{R}^{N\times N},B\in \mathbb{R}^{N\times 1} A ∈ R N × N , B ∈ R N × 1 c ( t ) c(t) c ( t ) f ≤ t f_{\leq t} f ≤ t
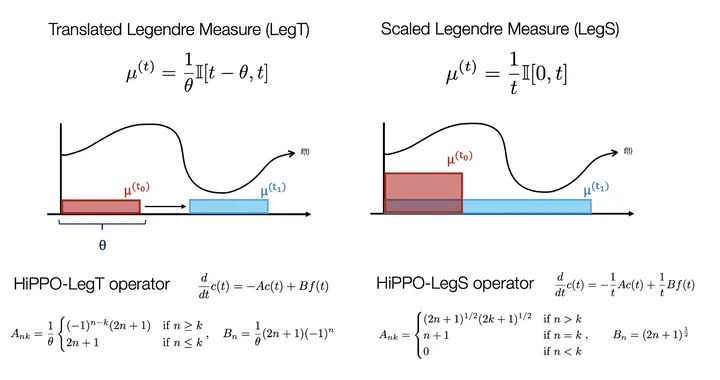
下面是一个实例,其中的蓝色线是 c ( t ) c(t) c ( t )
这两个 measure 都是在给定的窗口内的 uniform measures
第一个例子是 Translated Legendre Measure(LegT),它的 window size 是固定的,也就是说,它只在乎 recent history(within the window),而不在乎更早的 history。第二个例子是 scaled Legendre Measure(LegS),它的 window size 随着时间变换的,并且 window size 等于整个 history,所有的历史都同等重要。相应的,为了归一化,对每个时刻的 measure 的 scale 大小会对应缩放。
其中的 HiPPO 矩阵长这个样子:
上述连续的情形 c ˙ ( t ) = A ( t ) c ( t ) + B ( t ) f ( t ) \dot{c}(t)=A(t)c(t)+B(t)f(t) c ˙ ( t ) = A ( t ) c ( t ) + B ( t ) f ( t )
c t + 1 = A ˉ t c t + B ˉ t f t c_{t+1}=\bar{A}_{t} c_{t}+\bar{B}_{t} f_{t} c t + 1 = A ˉ t c t + B ˉ t f t 离散化的办法有很多,例如欧拉法,零阶保持等等。
采用如下公式来近似微分:
x ˙ = x ( k + 1 ) − x ( k ) T \dot{x}=\frac{x(k+1)-x(k)}{T} x ˙ = T x ( k + 1 ) − x ( k ) 欧拉法是一阶数值方法,取其曲线在 k k k
已知一定常连续系统的状态空间方程为:
{ x ˙ = A x + B u y = C x + D u \begin{cases}
\dot{\mathbf{x}}=\mathbf{A} \mathbf{x}+\mathbf{B} u \\
y=\mathbf{C x}+\mathbf{D} u
\end{cases} { x ˙ = Ax + B u y = Cx + D u 由 x ˙ = x ( k + 1 ) − x ( k ) T \dot{x}=\frac{x(k+1)-x(k)}{T} x ˙ = T x ( k + 1 ) − x ( k )
x ˙ = x ( k + 1 ) − x ( k ) T = A x ( k ) + B u ( k ) x ( k + 1 ) − x ( k ) = T [ A x ( k ) + B u ( k ) ] x ( k + 1 ) = ( I + T A ) x ( k ) + T B u ( k ) = Φ x ( k ) + G u ( k ) \begin{array}{l}
\dot{\mathbf{x}}=\frac{\mathbf{x}(k+1)-\mathbf{x}(k)}{T}=\mathbf{A} \mathbf{x}(k)+\mathbf{B} u(k) \\
\mathbf{x}(k+1)-\mathbf{x}(k)=T[\mathbf{A} \mathbf{x}(k)+\mathbf{B} u(k)] \\
\mathbf{x}(k+1)=(\mathbf{I}+T \mathbf{A}) \mathbf{x}(k)+T \mathbf{B} u(k)=\mathbf{\Phi} \mathbf{x}(k)+\mathbf{G} u(k)
\end{array} x ˙ = T x ( k + 1 ) − x ( k ) = Ax ( k ) + B u ( k ) x ( k + 1 ) − x ( k ) = T [ Ax ( k ) + B u ( k )] x ( k + 1 ) = ( I + T A ) x ( k ) + T B u ( k ) = Φx ( k ) + G u ( k ) 其中:Φ = I + T A ; G = T B \mathbf{\Phi}=\mathbf{I}+T \mathbf{A} ; \mathbf{G}=T \mathbf{B} Φ = I + T A ; G = T B
输出方程同样可以得到:
y = C x + D u ⇒ y ( k ) = H x ( k ) + J u ( k ) y=\mathbf{C x}+\mathbf{D} u \Rightarrow y(k)=\mathbf{H} \mathbf{x}(k)+\mathbf{J} u(k) y = Cx + D u ⇒ y ( k ) = Hx ( k ) + J u ( k ) 其中:H = C ; J = D \mathbf{H}=\mathbf{C} ; \mathbf{J}=\mathbf{D} H = C ; J = D
综上述,离散化后的状态空间为:
{ x ( k + 1 ) = Φ x ( k ) + G u ( k ) y ( k ) = H x ( k ) + J u ( k ) \begin{cases}
\mathbf{x}(k+1)=\boldsymbol{\Phi} \mathbf{x}(k)+\mathbf{G} u(k) \\
y(k)=\mathbf{H} \mathbf{x}(k)+\mathbf{J} u(k)
\end{cases} { x ( k + 1 ) = Φ x ( k ) + G u ( k ) y ( k ) = Hx ( k ) + J u ( k ) S4(Sequences With Structured State Spaces)
并行化加速
上述 HiPPO 构建了一个方法用于计算,估计系统矩阵 A \boldsymbol{A} A
为了并行化推理,我们 S4 引入了 SSM kernel。考虑输出 y 2 y_{2} y 2
y 2 = C h 2 = C ( A ˉ h 1 + B ˉ x 2 ) = C ( A ˉ ( A ˉ h 0 + B ˉ x 1 ) + B ˉ x 2 ) = C ( A ˉ ( A ˉ ⋅ B ˉ x 0 + B ˉ x 1 ) + B ˉ x 2 ) = C ( A ˉ ⋅ A ˉ ⋅ B ˉ x 0 + A ˉ ⋅ B ˉ x 1 + B ˉ x 2 ) = C ⋅ A ˉ A ˉ 2 ⋅ B ˉ x 0 + C ⋅ A ˉ ⋅ B ˉ ⋅ x 1 + C ⋅ B ˉ x 2 \begin{align}
y_{2} & = Ch_{2} \\
&=C\left(\bar{A} h_{1}+\bar{B} x_{2}\right) \\
&=C\left(\bar{A}\left(\bar{A} h_{0}+\bar{B} x_{1}\right)+\bar{B} x_{2}\right) \\
&=C\left(\bar{A}\left(\bar{A} \cdot \bar{B} x_{0}+\bar{B} x_{1}\right)+\bar{B} x_{2}\right) \\
&=C\left(\bar{A} \cdot \bar{A} \cdot \bar{B} x_{0}+\bar{A} \cdot \bar{B} x_{1}+\bar{B} x_{2}\right) \\
&=C \cdot \bar{A} \bar{A}^{2} \cdot \bar{B} x_{0}+C \cdot \bar{A} \cdot \bar{B} \cdot x_{1}+C \cdot \bar{B} x_{2}
\end{align} y 2 = C h 2 = C ( A ˉ h 1 + B ˉ x 2 ) = C ( A ˉ ( A ˉ h 0 + B ˉ x 1 ) + B ˉ x 2 ) = C ( A ˉ ( A ˉ ⋅ B ˉ x 0 + B ˉ x 1 ) + B ˉ x 2 ) = C ( A ˉ ⋅ A ˉ ⋅ B ˉ x 0 + A ˉ ⋅ B ˉ x 1 + B ˉ x 2 ) = C ⋅ A ˉ A ˉ 2 ⋅ B ˉ x 0 + C ⋅ A ˉ ⋅ B ˉ ⋅ x 1 + C ⋅ B ˉ x 2 由此类推,可得:
y 3 = C A A A B ‾ x 0 + C A A B ‾ x 1 + C A B ‾ x 2 + C B ‾ x 3 y_{3}=\mathbf{C} \overline{\mathbf{A A} \mathbf{A B}} x_{0}+\mathbf{C} \overline{\mathbf{A A B}} x_{1}+\mathbf{C} \overline{\mathbf{A B}} x_{2}+\mathbf{C} \overline{\mathbf{B}} x_{3} y 3 = C AA AB x 0 + C AAB x 1 + C AB x 2 + C B x 3 写成矩阵的形式可得:
y 3 = ( C A A A B ‾ C A A B ‾ C A ‾ B ‾ C B ‾ ) ( x 0 x 1 x 2 x 3 ) y_{3} = \begin{pmatrix}
\mathbf{C} \overline{\mathrm{AAAB}} & \mathbf{C} \overline{\mathrm{AAB}} & \mathbf{C} \overline{\mathbf{A}} \overline{\mathbf{B}} & \mathbf{C} \overline{\mathbf{B}}
\end{pmatrix} \begin{pmatrix}
x_{0} \\
x_{1} \\
x_{2} \\
x_{3}
\end{pmatrix} y 3 = ( C AAAB C AAB C A B C B ) x 0 x 1 x 2 x 3 其中矩阵 A , B , C A,B,C A , B , C
对角化
对于上述我们将我们需要计算矩阵的高次幂依然具有很高的复杂度,我们可以尝试对其进行对角化降低计算复杂度。
( A , B , C ) ∼ ( V − 1 A V , V − 1 B , C V ) (\boldsymbol{A}, \boldsymbol{B}, \boldsymbol{C}) \sim\left(\boldsymbol{V}^{-1} \boldsymbol{A} \boldsymbol{V}, \boldsymbol{V}^{-1} \boldsymbol{B}, \boldsymbol{C} \boldsymbol{V}\right) ( A , B , C ) ∼ ( V − 1 A V , V − 1 B , C V ) 如果上述 ( A , B , C ) (A,B,C) ( A , B , C ) y y y O ( N 2 ) \mathcal{O}(N^{2}) O ( N 2 ) O ( N ) \mathcal{O}(N) O ( N )
可以构造矩阵 A A A
A ~ = [ 1 − 1 2 1 − 3 3 ⋮ ⋮ ⋮ ⋱ ] \tilde{\boldsymbol{A}}= \begin{bmatrix}
1 & & & \\
-1 & 2 & & \\
1 & -3 & 3 & \\
\vdots & \vdots & \vdots & \ddots
\end{bmatrix} A ~ = 1 − 1 1 ⋮ 2 − 3 ⋮ 3 ⋮ ⋱ 即:
A n k ~ = { ( − 1 ) ( n − k ) ( 2 k + 1 ) if n > k k + 1 if n = k 0 if n < k \tilde{\boldsymbol{A}_{n k}} = \begin{cases}
(-1)^{(n-k)}(2 k+1) & \text { if } n>k \\
k+1 & \text { if } n=k \\
0 & \text { if } n<k
\end{cases} A nk ~ = ⎩ ⎨ ⎧ ( − 1 ) ( n − k ) ( 2 k + 1 ) k + 1 0 if n > k if n = k if n < k 那么可以找到一个可逆矩阵:
V = ( C i + j i − j ) i j = [ 1 1 1 1 3 1 ⋮ ⋮ ⋮ ⋱ ] \boldsymbol{V}=\left(C_{i+j}^{i-j}\right)_{i j}= \begin{bmatrix}
1 & & & \\
1 & 1 & & \\
1 & 3 & 1 & \\
\vdots & \vdots & \vdots & \ddots
\end{bmatrix} V = ( C i + j i − j ) ij = 1 1 1 ⋮ 1 3 ⋮ 1 ⋮ ⋱ 其中 V 3 i , i = C 4 i 2 i ≈ 2 4 i V_{3i,i}=C_{4i}^{2i}\approx 2^{4i} V 3 i , i = C 4 i 2 i ≈ 2 4 i
所以 S4 将矩阵 A \boldsymbol{A} A
A = V − 1 Λ V − P Q T = V − 1 ( Λ − ( V P ) ( P T V − 1 ) ) V \boldsymbol{A}=\boldsymbol{V}^{-1} \boldsymbol{\Lambda} \boldsymbol{V}-\boldsymbol{P} \boldsymbol{Q}^{T}=\boldsymbol{V}^{-1}\left(\boldsymbol{\Lambda}-(\boldsymbol{V} \boldsymbol{P})\left(\boldsymbol{P}^{T} \boldsymbol{V}^{-1}\right)\right) \boldsymbol{V} A = V − 1 Λ V − P Q T = V − 1 ( Λ − ( V P ) ( P T V − 1 ) ) V 其中 V ∈ R N × N \boldsymbol{V} \in \mathbb{R}^{N\times N} V ∈ R N × N Λ \Lambda Λ P , Q ∈ R N × r P,Q \in \mathbb{R}^{N\times r} P , Q ∈ R N × r (不懂这里如何得到的,逃)
Mamba
Mamba3
{ x ˙ = A x ( t ) + B μ ( t ) y = C x ( t ) \begin{cases}
\dot{\mathbf{x}} = \mathbf{A}x(t) + \mathbf{B}\mu(t) \\
y = \mathbf{C}x(t)
\end{cases} { x ˙ = A x ( t ) + B μ ( t ) y = C x ( t ) 其中的 ( A , B , C ) (\mathbf{A,B,C}) ( A , B , C )
在原本 S4 网络中其 A , B , C A,B,C A , B , C
原本矩阵 A \mathbf{A} A N × N N\times N N × N D × N D\times N D × N
这是因为矩阵 A \mathbf{A} A N N N × D \times D × D
而 Mamba 是利用 DNN 网络输出该矩阵:
S B ( x ) = Linear N ( x ) S C ( x ) = Linear N ( x ) S Δ ( x ) = Broadcast D ( Linear 1 ( x ) ) τ Δ = softplus \begin{array}{l}
S_{B}(x)=\operatorname{Linear}_{N}(x) \\
S_{C}(x)=\operatorname{Linear}_{N}(x) \\
S_{\Delta}(x)=\operatorname{Broadcast~}_{D}\left(\text { Linear }_{1}(x)\right) \\
\tau_{\Delta}=\text { softplus }
\end{array} S B ( x ) = Linear N ( x ) S C ( x ) = Linear N ( x ) S Δ ( x ) = Broadcast D ( Linear 1 ( x ) ) τ Δ = softplus 从而做到了与输入相关
为什么矩阵
A \mathbf{A} A 不是设计成网络的形式?
这是因为 A \mathbf{A} A A \mathbf{A} A τ Δ \tau_{\Delta} τ Δ A ˉ \bar{\mathbf{A}} A ˉ
并行化
上述变成时变后,我们就不能利用 SSM kernel 进行并行化。在 Mamba 中使用了一种 parallel scan 的技术。下方是 CUDA 关于该技术的介绍:
给定 n n n
[ a 0 , a 1 , … , a n − 1 ] [a_{0},a_{1},\dots,a_{n-1}] [ a 0 , a 1 , … , a n − 1 ] 求出序列
[ 1 , a 0 , ( a 0 ⊕ a 1 ) , … , ( a 0 ⊕ a 1 ⊕ ⋯ ⊕ a n − 2 ) ] [1,a_{0},(a_{0} \oplus a_{1}),\dots,(a_{0} \oplus a_{1}\oplus \dots \oplus a_{n-2})] [ 1 , a 0 , ( a 0 ⊕ a 1 ) , … , ( a 0 ⊕ a 1 ⊕ ⋯ ⊕ a n − 2 )] A Naive Parallel Scan
这个算法的效率在 O ( n log 2 ( n ) ) \mathcal{O}(n\log_{2}(n)) O ( n log 2 ( n ))
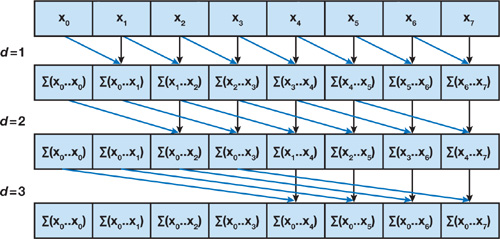
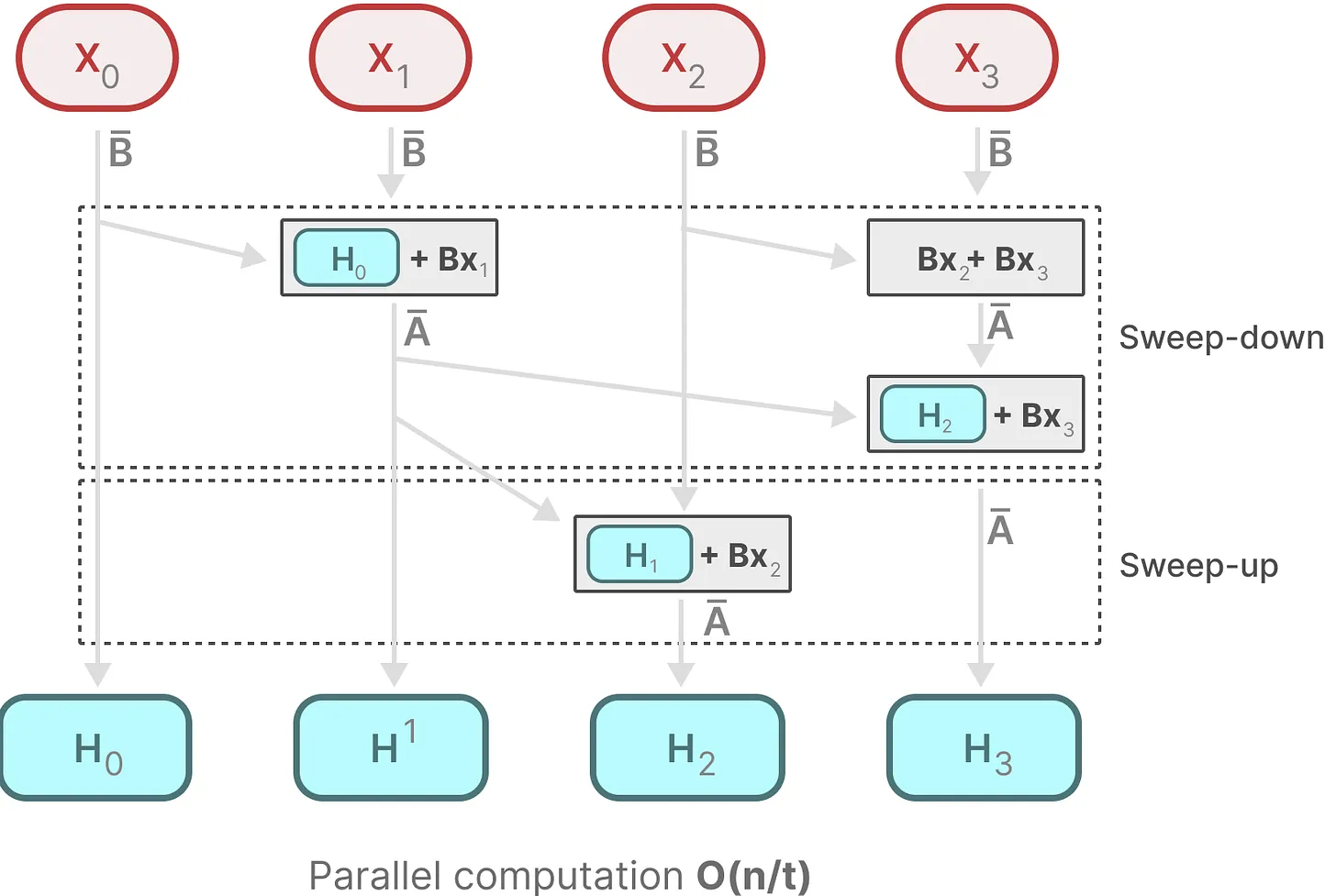
前缀和并行算法
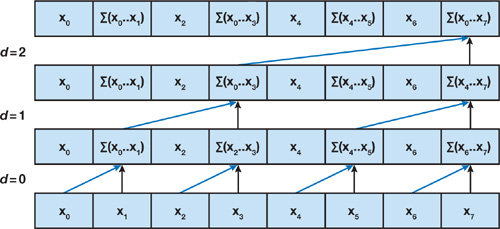
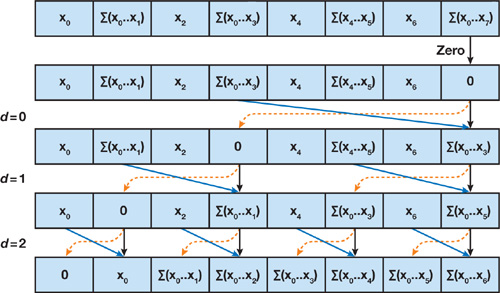
整个算法分为两个步骤,上扫和下扫。
在上扫过程,利用树形结构,相邻节点相加得到整个数组的和,而中间结果可以被后续过程所利用。
然后从上往下依次拼凑出前缀和。
而 Mamba 正是利用该算法实现了并行化训练
而上述的动态矩阵,并行扫描算法一起被叫做选择性扫描算法 (selective scan algorithm)
相关资料

 对序列进行展开:
对序列进行展开:
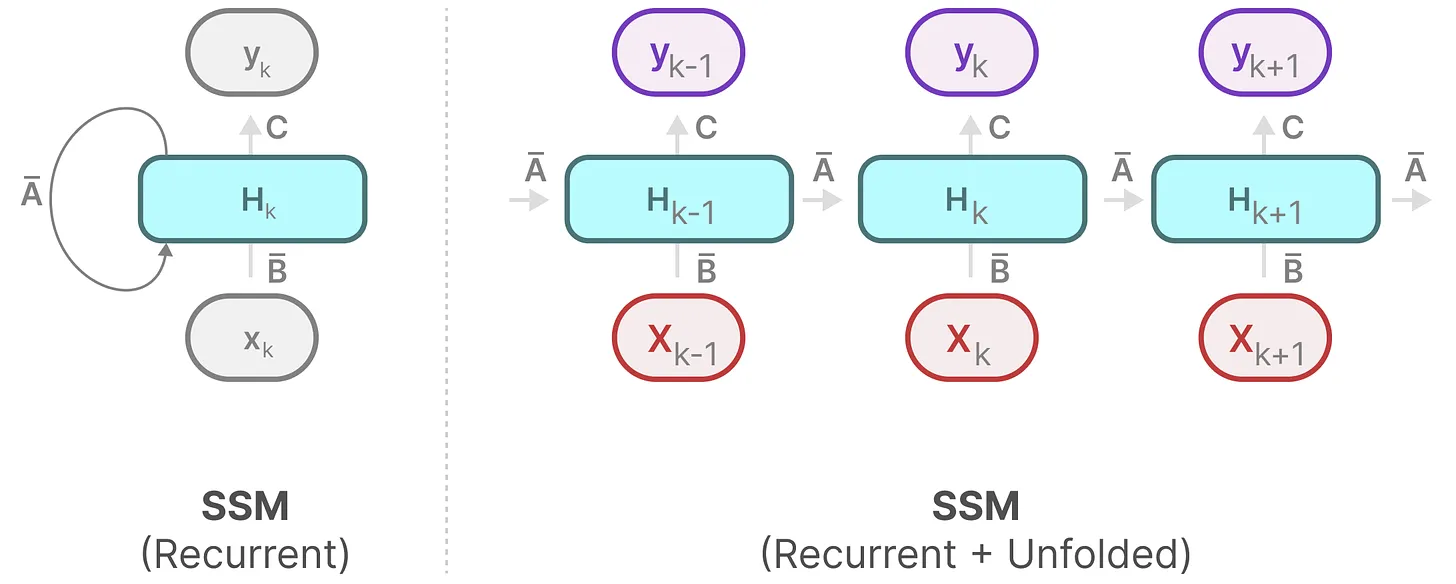
 而 Mamba 将该部分进行 ” 函数化 “,利用一个网络计算该部分。上图是二者的区别。
而 Mamba 将该部分进行 ” 函数化 “,利用一个网络计算该部分。上图是二者的区别。