Skip to main content

Legendre Transformations

· 5 min read
PuQing
PuQing
AI, CVer, Pythoner, Half-stack Developer
info

设函数 f:Rn→Rf:\mathbb{R}^n \to \mathbb{R}，定义函数 f∗:Rn→Rf^*:\mathbb{R}^n \to \mathbb{R} 则勒让德变换为：

f∗(s)=sup⁡x∈dom⁡f(sTx−f(x))f^*(s) = \sup_{x \in \operatorname{dom}f} \left( s^{\mathsf{T}}x-f(x)\right)

公式推导​

让我们暂时忘掉奇怪的符号，我们从一个单变量的函数 f(x)f(x) 开始。

简单来说，勒让德变换让函数 f(x)f(x) 转换成一个自变量为原函数导数的函数 f∗(s)f^*(s)

f(x)⇒f∗(dfdx)f(x) \Rightarrow f^*\left( \frac{df}{dx} \right)

而新函数的值实际是对应切线在 yy 轴的截距 bb

f∗(dffx)=−bf^*\left( \frac{df}{fx} \right) = -b
warning

这里我们加了一个负号，实际上没有任何区别

这就是勒让德变换的核心，你可能觉得这太随便了，但这是有原因的，实际上我们能够通过斜率和截距重构原函数 f(x)f(x)。

其完整的写法是：

f∗(dfdx)=dfdxx−ff^*\left( \frac{df}{dx} \right) = \frac{df}{dx}x-f

下面我们从几何直觉推导下：

warning

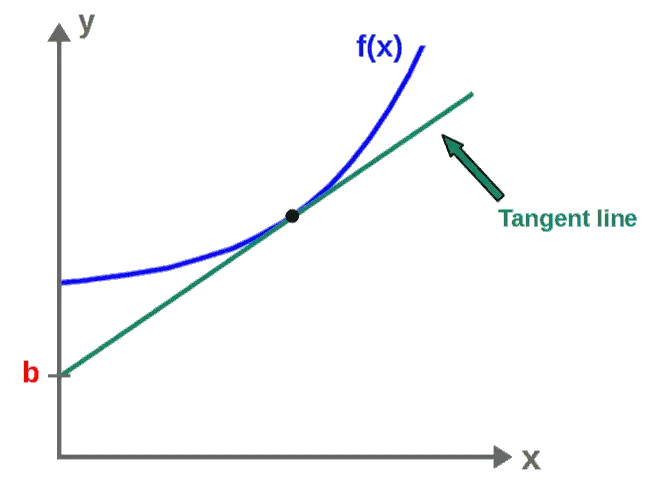image.png 我们想要求解截距 bb

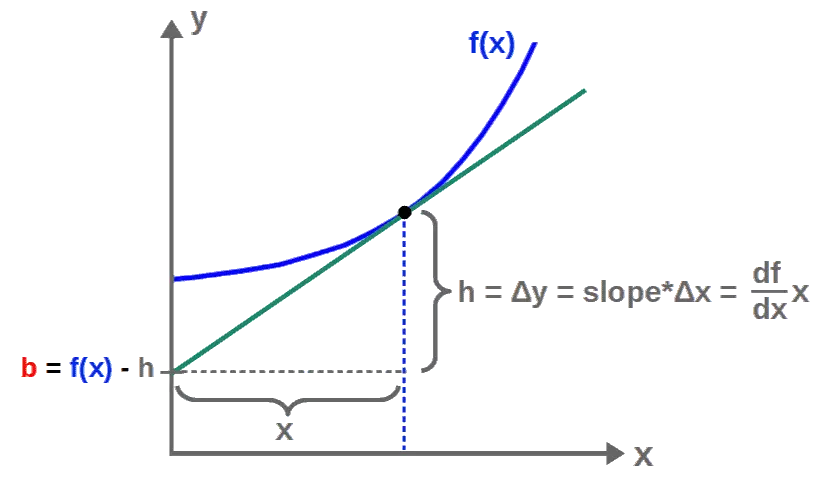image.png 于是

b=f−dfdxxb=f-\frac{df}{dx}x

所以

f∗(dfdx)=−b=dfdxx−ff^*\left( \frac{df}{dx} \right)=-b=\frac{df}{dx}x-f
例子

对于简单函数 f(x)=x2f(x)=x^{2}，我们首先定义新的自变量 pp

p=dfdx=2xp=\frac{df}{dx}=2x

我们可以解得：

p=2x⇒x(p)=p2p=2x \Rightarrow x(p)=\frac{p}{2}

f(x)f(x) 带入 x(p)x(p) 得到 f(p)f(p)

f(x)=x2⇒f(p)=(p2)2=p44f(x) = x^{2} \Rightarrow f(p) = \left( \frac{p}{2} \right)^{2} = \frac{p^{4}}{4}

于是函数 f(x)=x2f(x)=x^{2} 的勒让德变换为：

f∗(p)=px(p)−f(p)=pp2−p24=p24f^*(p) = px(p)-f(p) = p \frac{p}{2} -\frac{p^2}{4} = \frac{p^{2}}{4}

你搁着套娃呢​

我们对 f∗f^* 求斜率

df∗(p)dp=ddfdxx−fddfdx=x\frac{df^*(p)}{dp} =\frac{d \frac{df}{dx}x-f}{d \frac{df}{dx}} =x

可以得到 f∗(p)f^*(p) 的斜率是 xx，而 f(x)f(x) 的斜率是 pp，（奇妙的对偶）

如果说，我们想找到 f(x)f(x) 的最小值，并且我们有共轭函数 f∗(p)f^*(p)，只需要在最小值处，让切线斜率为 00（函数性质良好）。那不正好对应了共轭函数的原点了吗

f∗(0)=0Txmin⁡−f(xmin⁡)f(xmin⁡)=−f∗(0)\begin{split} f^*(0) = 0^{\mathsf{T}} x_{\min}-f(x_{\min})\\ f(x_{\min}) = - f^*(0) \end{split}

Legendre-Fenchel Transform​

Legendre 变换本身很有用，但是它仅仅局限在凸函数和可微函数，如果这两个条件有一个不满足，那么这个变换就无法完成。让我们考虑 f(x)=∣x∣f(x)=\mid x\mid。函数斜率在 x=0x=0 处没有定义。如下图所示。 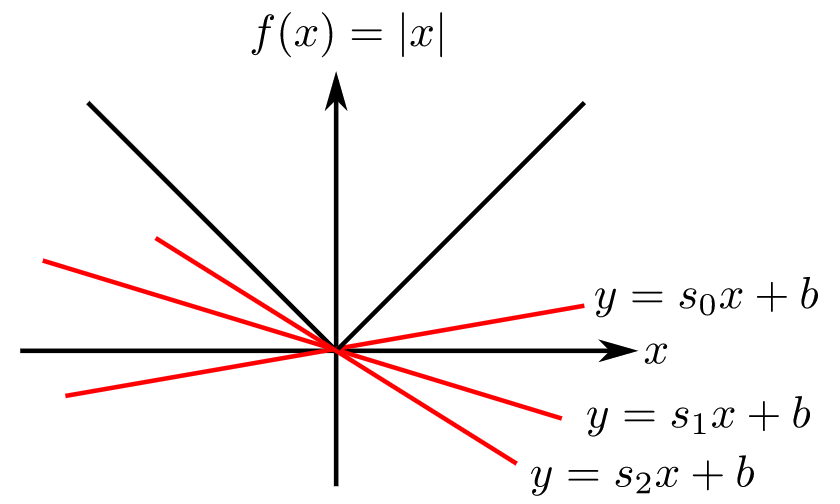image.png 另外，非凸函数在不同点处其斜率的可能相同，这导致 xx 和 pp 之间不存在唯一的对应关系。如下图，同一个斜率 pp 可能对应则两个 bb 值。 image.png

而 Fenchel\text{Fenchel} 找到了一个巧妙的转换技巧，将 Legendre\text{Legendre} 变换推广到了这类函数中。

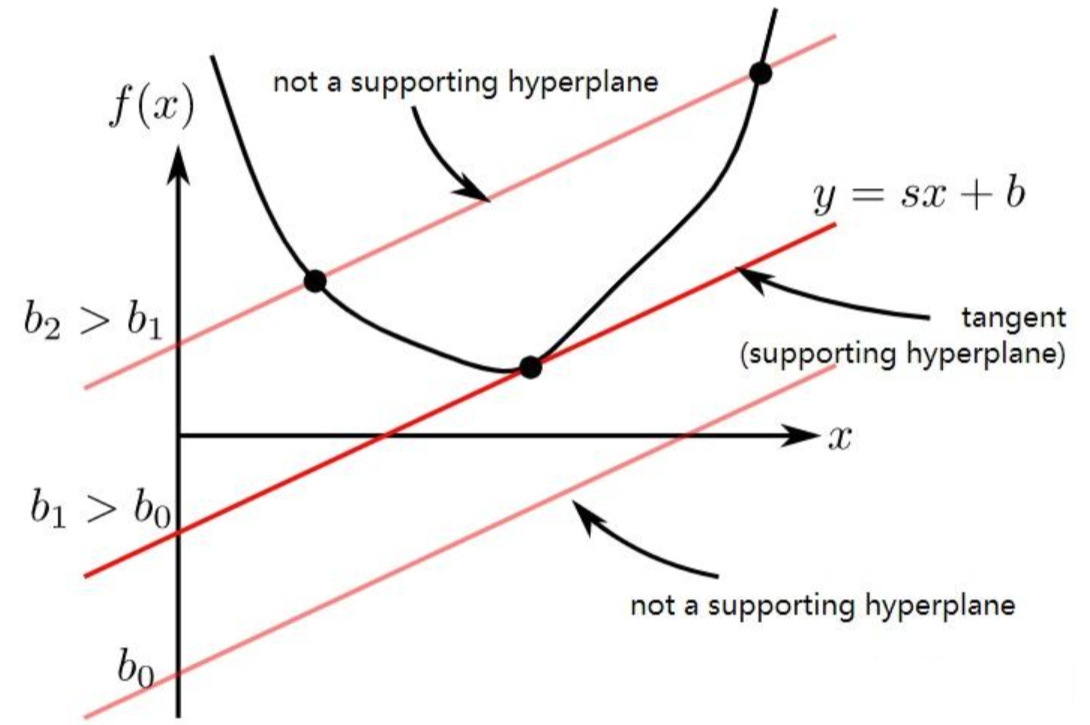
我们将共轭函数 f∗(p)f^*(p) 的值等价于寻找斜率为 pp 的切线截距 bb，它是斜率为 pp 的直线穿过凸函数与 yy 轴相交的最小截距，如下图所示： image.png

可以看到拥有最小截距的直线只是众多直线中的一条，小于该截距时，直线将不与 f(x)f(x) 相交，因此在更多的时候，我们通常选一组与 f(x)f(x) 相交的直线，然后寻找最小截距的那条。这使得不可微甚至是非凸函数也可以使用这一变换：

此时，我们想要对于所有的 xx 来说最小的 bb，那么有

b=inf⁡x(f(x)−sTx)=inf⁡x(−(sTx−f(x)))=−sup⁡x(sTx−f(x))\begin{split} b &= \inf_{x}\left( f(x)-s^{\mathsf{T}}x \right) \\ &= \inf_{x} \left( -(s^{\mathsf{T}}x-f(x)) \right) \\ &= -\sup_{x} \left( s^{\mathsf{T}}x-f(x) \right) \end{split}
tip

这里使用了性质 inf⁡(−x)=−sup⁡(x)\inf(-x)=-\sup(x)

于是我们最终得到：

f∗(s)=−b=sup⁡x(sTx−f(x))f^*(s)= -b = \sup_{x}(s^{\mathsf{T}}x-f(x))
info

讨论 Bregmen Divergence\text{Bregmen Divergence}

相关资料​