强化学习 - 基本组件

info

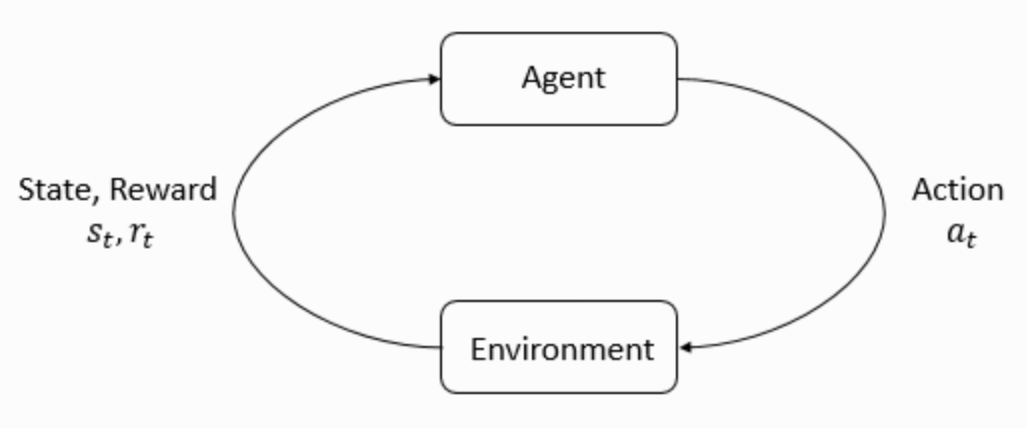
The main characters of RL are the agent and the environment. The environment is the world that the agent lives in and interacts with. At every step of interaction, the agent sees a (possibly partial) observation of the state of the world, and then decides on an action to take. The environment changes when the agent acts on it, but may also change on its own.

The agent also perceives a reward signal from the environment, a number that tells it how good or bad the current world state is. The goal of the agent is to maximize its cumulative reward, called return. Reinforcement learning methods are ways that the agent can learn behaviors to achieve its goal.

States and Observations

状态 $S$ 的一个关于这个世界状态的完整描述。观察 $O$ 是对于状态的部分描述。比如视觉上的观察可以用 RGB 矩阵来表述。机器人的角速度等可以用状态进行表述。

Action Spaces

不同的环境有不同的动作。所有有效动作的集合称之为 动作空间。有些环境，比如说 Atari 游戏和围棋，属于 离散动作空间，这种情况下智能体只能采取有限的动作。其他的一些环境，比如智能体在物理世界中控制机器人，属于 连续动作空间。在连续动作空间中，动作是实数向量。

Policies

策略 是智能体用于决定下一步执行什么行动的规则。可以是确定性的，一般表示为：$\mu$

$$a_{t} = \mu_{t}(s_{t})$$

也可以是随机的，

$$a_{t} \sim \pi(\cdot \mid s_{t})$$

在深度强化学习中，我们处理的是参数化的策略，这些策略的输出，依赖于一系列计算函数，而这些函数又依赖于参数（例如神经网络的权重和误差），所以我们可以通过一些优化算法改变智能体的的行为。

我们经常把这些策略的参数写作 $\theta$ 或者 $\phi$ ，所以上述公式可以写作：

$$\begin{aligned} a_{t} & =\mu_{\theta}\left(s_{t}\right) \\ a_{t} & \sim \pi_{\theta}\left(\cdot \mid s_{t}\right) \end{aligned}$$

Deterministic Policies

Example: Deterministic Policies. Here is a code snippet for building a simple deterministic policy for a continuous action space in PyTorch, using the torch.nn package:

pi_net = nn.Sequential(
		  nn.Linear(obs_dim, 64),
		  nn.Tanh(),
		  nn.Linear(64, 64),
		  nn.Tanh(),
		  nn.Linear(64, act_dim)
        )

If obs is a Numpy array containing a batch of observations, pi_net can be used to obtain a batch of actions as follows:

obs_tensor = torch.as_tensor(obs, dtype=torch.float32)
actions = pi_net(obs_tensor)

Stochastic Policies

最常用的两种强化学习随机策略是 categorical policies and diagonal Gaussian policies.

Categorical policies 主要被用于离散动作空间中，而 diagonal Gaussian policies 被用于连续动作空间中

使用 Stochastic policies 最重要的两个计算地方就是；

• 从 policy 中采样
• 计算动作的对数似然 (log likelihoods),$\log \pi_{\theta}(a\mid s)$

Categorical Policies

A categorical policy is like a classifier over discrete actions. You build the neural network for a categorical policy the same way you would for a classifier: the input is the observation, followed by some number of layers (possibly convolutional or densely-connected, depending on the kind of input), and then you have one final linear layer that gives you logits for each action, followed by a softmax to convert the logits into probabilities.

Sampling: 根据每个动作的概率，我们就可以通过采样得到下一步的动作是什么。

Log-Likelihood. 我们将上面网络最后一层输出的概率记作为：$P_{\theta}(s)$，这是一个向量，这个向量的 index 表示该动作的概率，所以动作 $a$ 的对数似然为 $\log \pi_{\theta}(a\mid s)=\log \left[ P_{\theta}(s) \right]_{a}$

Trajectories

运动轨迹 $\tau$ 被记作为一个在世界中状态和动作的序列，

$$\tau = (s_{0},a_{0},s_{1},a_{1},\dots).$$

最初的状态 $s_{0}$ 是一个从初始状态分布中采样得到。记作为：

$$s_{0} \sim \rho_{0}(\cdot).$$

状态转换 $s_{t}\to s_{t+1}$ 是由环境所确定的，并且只依赖最近的行动 $a_{t}$（马尔可夫性质）。这个转换可以是确定的，

$$s_{t+1} = f(s_{t},a_{t})$$

也可以是随机的，

$$s_{t+1} \sim P(\cdot\mid s_{t},a_{t})$$

info

Trajectories 常常也被称作 回合 (episodes) 或者 rollouts。

Reward and Return

强化学习中，奖励函数 $R$ 非常重要。它由当前状态、已经执行的行动和下一步的状态共同决定。

$$r_{t}=R\left(s_{t}, a_{t}, s_{t+1}\right)$$

有时候这个公式会被改成只依赖当前的状态 $r_{t}=R(s_{t})$，或者状态行动对 $r_{t}=R(s_{t},a_{t})$

智能体的目标是最大化行动轨迹的累计奖励，对于此我们可以统一表达为 $R(\tau)$。

$T$ 步累计奖励，指的是在一个固定窗口步数 $T$ 内获得的累计奖励：

$$R(\tau)=\sum_{t=0}^{T} r_{t}$$

另一种叫做 $\gamma$ 折扣奖励，指的是智能体获得的全部奖励之和，但是奖励会因为获得的时间不同而衰减。这个公式包含衰减率 $\gamma \in (0,1)$

$$R(\tau)=\sum_{t=0}^{\infty} \gamma^{t} r_{t}$$

这里为什么要加上一个衰减率呢？为什么不直接把所有的奖励加在一起？可以从两个角度来解释： 直观上讲，现在的奖励比外来的奖励要好，所以未来的奖励会衰减；数学角度上，无限多个奖励的和很可能不收敛，有了衰减率和适当的约束条件，数值才会收敛。

The RL Problem

无论选择哪种方式衡量收益（$T$ 步累计奖赏或者 $\gamma$ 折扣奖励），无论选择哪种策略，强化学习的目标都是选择一种策略从而最大化 预期收益。

我们假设环境转换和策略都是随机的。这种情况下，$T$ 步的动作轨迹是：

$$P(\tau \mid \pi)=\rho_{0}\left(s_{0}\right) \prod_{t=0}^{T-1} P\left(s_{t+1} \mid s_{t}, a_{t}\right) \pi\left(a_{t} \mid s_{t}\right)$$

拆解

首先是因为初始状态是随机的，所以 $s_{0}$ 概率为 $\rho_{0}(s_{0})$，之后过程为：

$$$$

$$\begin{cases} T=0 \text{时}: \text{模型预测动作}a_{0} \text{，其概率为} \pi(a_{0}\mid s_{0}), \text{环境根据动作更新状态，所以概率为} P(s_{1}\mid s_{0},a_{0}) \\ T=1 \text{时}: \text{模型预测动作}a_{1} \text{，其概率为} \pi(a_{1}\mid s_{1}), \text{环境根据动作更新状态，所以概率为} P(s_{2}\mid s_{1},a_{1}) \\ \dots \end{cases}$$

假设整个系统具有马尔可夫性

所以整个动作轨迹的概率分布即为上述公式 (整个公式的含义为在模型 $\pi$ 下，运动轨迹为 $\tau$ 的概率)。

于是预期收益为：

$$J(\pi)=\int_{\tau} P(\tau \mid \pi) R(\tau)=\underset{\tau \sim \pi}{\mathrm{E}}[R(\tau)]$$

解释

因为我们假设策略是随机的，所以这里是概率积分的形式

强化学习中的核心优化问题可以表示为：

$$\pi^{*}=\arg \max _{\pi} J(\pi)$$

$\pi^{*}$ 是最优策略