二自由度运动方程及逆运动反求

问题定义

如图，背景暂时不介绍了，其中 $\beta$ 定义为在坐标轴 $x-y$ 上的旋转方向，而 $\alpha$ 定义为在坐标轴 $x-z$ 上的旋转角度。

激光源的定义

这样光源点可以表征为：

$$P_{0}=(0,0,h)$$

其中 $h$ 为云台高度，为内参。

而激光发射的方向向量可以通过两个旋转角度进行表示：

$$\vec{v}=(\cos \beta,\sin \beta,\sin \alpha)$$

于是便可以通过点向式对射线进行表达：

$$\frac{x}{\cos \beta}=\frac{y}{\sin \beta}=\frac{z-h}{\sin \alpha}$$

显然需要约束，即 $x>0$

屏幕的定义

显然，在上述坐标系中，屏幕可以被描述为：

$$\Omega = (1,y,z), \quad y\in(-0.25,0.25), z\in(h-0.25,h+0.25)$$

请注意

该方程是有假设的，即在光源对准屏幕的中心点时是无仰角，无旋转的，如果不明白，可以看下图：

理想情况下逆运动反求

已知对于激光射在屏幕上某一点 $(1,y,z)$，则可以反推回光源点处的参数状态：

利用上式射线方程，可得方程组

$$\frac{1}{\cos \beta}=\frac{y}{\sin \beta} =\frac{z-h}{\sin \alpha}$$

求得参数为：

$$\begin{cases} \alpha = - \arcsin\left(\displaystyle \frac{h}{\sqrt{ 1+y^2 }}-\frac{z}{\sqrt{ 1+y^2 }} \right), \\ \beta_{1} = \arctan\left( \displaystyle \frac{1}{\sqrt{ 1+y^2 }} \right), \\ \beta_{2} = \arctan\left( \displaystyle \frac{y}{\sqrt{ 1+y^2 }} \right), \end{cases}$$

我们不妨带入一些特殊值，用以验证准确性，对于屏幕中心点有坐标 $(1,0,h)$

代入上式，得：

$$\begin{cases} \alpha = -\arcsin(0) =0,\\ \beta_{1} = \arctan(1) = 45\degree,\\ \beta_{2} = \arctan(0) = 0. \end{cases}$$

所以其解 $\beta_{1}$ 为错误解，略去，下面取 $\alpha,\beta_{2}$ 作为标准解。

如果我们已知屏幕点 $p$ 的运动方程，我们可以通过上面的标准解得到参数控制方程。

知识补充

正方形的隐函数方程为

$$\mid x\mid +\mid y\mid =1$$

可是该正方形不是正的，而是 " 歪的 "，如下图

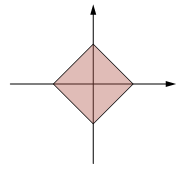
其参数方程为

$$(\cos(t)\cdot \left | \cos(t) \right |,\sin(t)\cdot \left | \sin(t) \right |)$$

为了 " 掰正 "，我们使用旋转矩阵

$$\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix}= \begin{bmatrix} \cos (\theta ) & -\sin (\theta) & 0\\ \sin (\theta )& \cos (\theta ) & 0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$$

其中的 $\theta$ 为旋转角度，这里为 $45\degree$。

所以参数方程转化为：

$$\begin{bmatrix} x(t) \\ y(t) \end{bmatrix}=\begin{bmatrix} \frac{\sqrt{2}}{2}( \cos (t)|\cos (t)|-\sin (t)|\sin (t)|) \\ \frac{\sqrt{2}}{2}(\sin (t) |\sin (t)|+\cos (t)|\cos (t)|) \end{bmatrix}$$

就离谱啊

warning

注意，这里是单位正方形，如果是其他正方形需要乘以系数

info

根据上面知识，已知点 $p$ 满足下面正方形参数方程：

$$\begin{cases} x = 1 \\ y = \frac{1}{2}( \cos (t)\cdot |\cos (t)|-\sin (t)\cdot |\sin (t)|) \\ z = \frac{1}{2}(\sin (t)\cdot |\sin (t)|+\cos (t)\cdot |\cos (t)|)+h \end{cases}$$

有点崩溃，人傻了 (上面方程已乘以系数，请注意这个 $h$)

代入上述标准解中？？，解得

$$\begin{cases} \alpha = \operatorname{asin}{\left(\displaystyle \frac{\sin{\left(t \right)} \left|{\sin{\left(t \right)}}\right| + \cos{\left(t \right)} \left|{\cos{\left(t \right)}}\right|}{\sqrt{\left(\sin{\left(t \right)} \left|{\sin{\left(t \right)}}\right| - \cos{\left(t \right)} \left|{\cos{\left(t \right)}}\right|\right)^{2} + 4}} \right)} \\ \beta = - \operatorname{atan}{\left(\displaystyle \frac{\sin{\left(t \right)} \left|{\sin{\left(t \right)}}\right| - \cos{\left(t \right)} \left|{\cos{\left(t \right)}}\right|}{\sqrt{\left(\sin{\left(t \right)} \left|{\sin{\left(t \right)}}\right| - \cos{\left(t \right)} \left|{\cos{\left(t \right)}}\right|\right)^{2} + 4}} \right)} \end{cases}$$

太过于繁杂，不妨令：

$$\begin{cases} t_{1} = \sin{\left(t \right)} \left|{\sin{\left(t \right)}}\right|\\ t_{2} = \cos{\left(t \right)} \left|{\cos{\left(t \right)}}\right| \end{cases}$$

则上面式子可以写为：

$$\begin{cases} \alpha = \arcsin \left( \displaystyle \frac{t_{1}+t_{2}}{\sqrt{ (t_{1}-t_{2})^2 +4}} \right) \\ \beta = -\arctan\left(\displaystyle \frac{t_{1}-t_{2}}{\sqrt{ (t_{1}-t_{2})^2 +4}}\right) \end{cases}$$

至此，我们已经纯靠求解的方式解出控制参数 $\alpha,\beta$ 的控制方程。理论上，对参数施以上述控制方程，应能在屏幕上看到正方形。(不行了，好饿，不知道有没有求错)。

该解非常自然，因为其中消掉了云台高度 $h$，这也是非常自然的 (因为实际上可以已出光点建立坐标系，自然没有了 $h$)

一般情况下逆运动反求

对于一般情况，可能激光源对准时并非理想状态，即有仰角，有旋转，这时如何求解呢？

下面是建模图

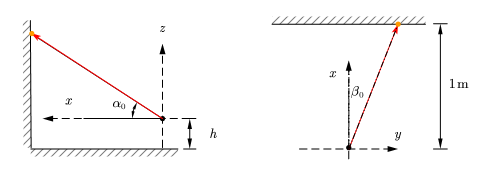
即在初始对齐时，激光源具有仰角 $\alpha_{0}$，旋转角 $\beta_{0}$

这会改变我们什么呢？

射线方程？不是，射线方程只与红激光发射位置有关。没错，是正方形的参数方程。

在理想情况下，其假设的屏幕是对齐云台 $x,y$ 轴的。可是现实情况可能没那么理想，所以我们需要修正上述的正方形参数方程。

修正后的正方形参数方程：

$$\begin{cases} x = 1 \\ y =\displaystyle \frac{1}{2}( \cos (t)\cdot |\cos (t)|-\sin (t)\cdot |\sin (t)|) +\tan(\beta_{0}) \\ z =\displaystyle \frac{1}{2}(\sin (t)\cdot |\sin (t)|+\cos (t)\cdot |\cos (t)|)+h +\tan(\alpha_{0}) \end{cases}$$

其中的 $\alpha_{0},\beta_{0}$ 即为初始对齐状态的仰角以及旋转角，重新代入到标准解，解得：

$$\begin{cases} \alpha = \operatorname{asin}{\displaystyle \left(\frac{\sin{\left(t \right)} \left|{\sin{\left(t \right)}}\right| + \cos{\left(t \right)} \left|{\cos{\left(t \right)}}\right| + 2 \tan{\left(\alpha_{0} \right)}}{\sqrt{\left(- \sin{\left(t \right)} \left|{\sin{\left(t \right)}}\right| + \cos{\left(t \right)} \left|{\cos{\left(t \right)}}\right| + 2 \tan{\left(\beta_{0} \right)}\right)^{2} + 4}} \right)} \\ \beta = \operatorname{atan}{\left(\displaystyle \frac{- \sin{\left(t \right)} \left|{\sin{\left(t \right)}}\right| + \cos{\left(t \right)} \left|{\cos{\left(t \right)}}\right| + 2 \tan{\left(\beta_{0} \right)}}{\sqrt{\left(- \sin{\left(t \right)} \left|{\sin{\left(t \right)}}\right| + \cos{\left(t \right)} \left|{\cos{\left(t \right)}}\right| + 2 \tan{\left(\beta_{0} \right)}\right)^{2} + 4}} \right)} \end{cases}$$

同样的令 $t_{1},t_{2}$，化简得到：

$$\begin{cases} \alpha = \operatorname{asin}{\displaystyle \left(\frac{t_{1} + t_{2} + 2 \tan{\left(\alpha_{0} \right)}}{\sqrt{\left(- t_{1} + t_{2} + 2 \tan{\left(\beta_{0} \right)}\right)^{2} + 4}} \right)} \\ \beta = \operatorname{atan}{\displaystyle \left(\frac{- t_{1} + t_{2} + 2 \tan{\left(\beta_{0} \right)}}{\sqrt{\left(- t_{1} + t_{2} + 2 \tan{\left(\beta_{0} \right)}\right)^{2} + 4}} \right)} \end{cases}$$

这个解同样十分自然

推广

对于其他位置，其他形状可以利用上述过程进行求解，其关键点在于对准几何体的几何中心。

注意

对于旋转了的几何体，可以通过 CV 等方式获得旋转角度内参，并运用旋转矩阵，使之转化为一般情况。