Skip to main content

高斯分布

· 8 min read
PuQing
PuQing
AI, CVer, Pythoner, Half-stack Developer

假设有数据：

X=(x1,x2,⋯ ,xN)T=(x1Tx2T⋮xNT)=(x11x12…x1px21x32…x2p⋮⋮⋱⋮xN1xN2…xNp)N×PX=\left(x_{1}, x_{2}, \cdots, x_{N}\right)^{T}=\left(\begin{array}{c} x_{1}^{T} \\ x_{2}^{T} \\ \vdots \\ x_{N}^{T} \end{array}\right)=\left(\begin{array}{cccc} x_{11} & x_{12} & \ldots & x_{1 p} \\ x_{21} & x_{32} & \ldots & x_{2 p} \\ \vdots & \vdots & \ddots & \vdots \\ x_{N 1} & x_{N 2} & \ldots & x_{N p} \end{array}\right)_{N \times P}

其中 xi∈Rpx_{i}\in \mathbb{R}^p，xi∼N(μ,Σ)x_{i} \sim \mathcal{N}(\mu, \Sigma)，参数为 θ=(μ,Σ)\theta=(\mu,\Sigma)

单变量高斯分布​

对于单变量的高斯分布 N(μ,σ2)\mathcal{N}(\mu,\sigma^2)，即 p=1p=1，其概率密度函数为

p(x)=12πσexp⁡{−(x−μ)22σ2}p(x)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left\{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right\}

我们希望通过观察到的数据来计算参数 θ\theta 的值，使用 极大似然估计 进行估计，似然函数可以写为

log⁡p(X;θ)=log⁡∏i=1Np(xi;θ)=∑i=1Nlog⁡p(xi;θ)=∑i=1N[log⁡12π+log⁡1σ−(xi−μ)22σ2]\begin{aligned} \log p(X ; \theta) & =\log \prod_{i=1}^{N} p\left(x_{i} ; \theta\right)=\sum_{i=1}^{N} \log p\left(x_{i} ; \theta\right) \\ & =\sum_{i=1}^{N}\left [ \log \frac{1}{\sqrt{2 \pi}}+\log \frac{1}{\sigma}-\frac{(x_{i}-\mu)^{2}}{2 \sigma^{2}} \right ] \end{aligned}

求解参数​

warning

对于 μ\mu 的估计实际上就是：

μMLE=arg⁡max⁡μlog⁡p(X;θ)=arg⁡max⁡μ∑i=1N−(xi−μ)22σ2(省略无关项)=arg⁡min⁡μ∑i=1N(xi−μ)2\begin{split} \mu_{\text{MLE}} &= \arg \max_{\mu} \log p(X;\theta)\\ &=\arg \max_{\mu} \sum_{i=1}^N -\frac{(x_{i}-\mu)^{2}}{2 \sigma^{2}} \quad \quad (\text{省略无关项})\\ &=\arg \min_{\mu} \sum_{i=1}^N (x_{i}-\mu)^2 \end{split}

对其求导得到：

∂∂μ∑i=1N(xi−μ)2=∑i=1N2⋅(xi−μ)⋅(−1)=0\frac{\partial}{\partial \mu} \sum_{i=1}^N(x_{i}-\mu)^2 = \sum_{i=1}^N 2\cdot(x_{i}-\mu) \cdot(-1) = 0

解得：

∑i=1Nxi=∑i=1NμμMLE=1N∑i=1Nxi\begin{split} \sum_{i=1}^N x_{i} &= \sum_{i=1}^N \mu \\ \mu_{\text{MLE}} &= \frac{1}{N} \sum_{i=1}^N x_{i} \end{split}
warning
σMLE2=arg⁡max⁡σlog⁡p(X;θ)=arg⁡max⁡σ∑i=1N[log⁡1σ−(xi−μ)22σ2]\begin{split} \sigma^2_{\text{MLE}} &= \arg \max_{\sigma} \log p(X;\theta) \\ &= \arg \max_{\sigma} \sum_{i=1}^N \left[ \log \frac{1}{\sigma}- \frac{(x_{i}-\mu)^2}{2\sigma^2} \right]\\ \end{split}

求导得：

∂log⁡p(x;θ)∂σ=∑i=1N−1σ−12(xi−μ)2(−2)σ−3=0\frac{\partial \log p(x;\theta)}{\partial \sigma} = \sum_{i=1}^{N}-\frac{1}{\sigma}-\frac{1}{2}\left(x_{i}-\mu\right)^{2}(-2) \sigma^{-3}=0

解得：

∑i=1Nσ2=∑i=1N(xi−μ)2\sum_{i=1}^{N} \sigma^{2}=\sum_{i=1}^{N}\left(x_{i}-\mu\right)^{2}σMLE2=1N∑i=1N(xi−μ)2\sigma_{M L E}^{2}=\frac{1}{N} \sum_{i=1}^{N}\left(x_{i}-\mu\right)^{2}

而这里是含 μ\mu 的，所以是 μMLE\mu_{MLE}.

σMLE2=1N∑i=1N(xi−μMLE)2\sigma_{M L E}^{2}=\frac{1}{N} \sum_{i=1}^{N}\left(x_{i}-\mu_{M L E}\right)^{2}

无偏性​

无偏估计就是 E(x^)=x\mathbb{E}(\hat{x})=x，下面我们分别判断上述 μMLE,σMLE\mu_{\text{MLE}},\sigma_{\text{MLE}} 的无偏性。

E[μMLE]=E[1N∑i=1Nxi]=1N∑i=1NE[xi]=1NNμ=μ\begin{aligned} \mathbb{E}\left[\mu_{M L E}\right] & =\mathbb{E}\left[\frac{1}{N} \sum_{i=1}^{N} x_{i}\right] \\ & =\frac{1}{N} \sum_{i=1}^{N} \mathbb{E}\left[x_{i}\right] \\ & =\frac{1}{N} N \mu=\mu \end{aligned}
info

所以 μ\mu 是无偏估计

可以化简一下 σ\sigma 的估计

σMLE2=1N∑i=1N(xi−μMLE)2 =1N∑i=1N(xi2−2μMLExi+μMLE2) =1N∑i=1Nxi2−2⋅μMLE⋅1N∑iNxi⏟μMLE+1N∑i=1NμMLE2 =1N∑i=1N(xi2−μMLE2)\begin{aligned} \sigma_{\text{MLE}}^2 &= \frac{1}{N} \sum_{i=1}^N (x_{i}-\mu_{\text{MLE}})^2\ &= \frac{1}{N} \sum_{i=1}^{N}\left(x_{i}^{2}-2 \mu_{M L E} x_{i}+\mu_{M L E}^{2}\right) \ &= \frac{1}{N} \sum_{i=1}^{N}x_{i}^{2} -2 \cdot\mu_{M L E} \cdot \underbrace{\frac{1}{N} \sum_{i}^N x_{i}}_{{\color{Red} \mu_{\text{MLE} } }} +\frac{1}{N} \sum_{i=1}^{N}\mu_{M L E}^{2}\ &= \frac{1}{N} \sum_{i=1}^N \left( x_{i}^2 -\mu_{\text{MLE}}^2\right) \end{aligned}

于是期望是

E[σMLE2]=E[1N∑i=1N(xi2−μMLE2)]=E[1N∑i=1N(xi2−μ2)−(μMLE2−μ2)]=E[1N∑i=1N(xi2−μ2)]−E[(μMLE2−μ2)]=1N∑i=1NE[xi2−μ2]−E[μMLE2−μ2]=1N∑i=1N(E[xi2]−μ2⏟Var(xi)=σ2)−E[μMLE2−μ2](Var(X)=E[X2]−E2(X))=σ2−E[μLE2−μ2]=σ2−E[μLE2]−E[μ2]=σ2−E[μLE2]−μ2=σ2−E[μLE2]−E2[μMLE]⏟Var[μMLE]=σ2−Var⁡[1N∑i=1Nxi]=σ2−1N2∑i=1NVar⁡[xi](Var(CX)=D2Var(X))=σ2−1N2Nσ2=N−1Nσ2\begin{split} \mathbb{E}\left[\sigma_{M L E}^{2}\right] &= \mathbb{E} \left[ \frac{1}{N} \sum_{i=1}^N \left( x_{i}^2 -\mu_{MLE}^2\right) \right]\\ &= \mathbb{E}\left[\frac{1}{N} \sum_{i=1}^{N}\left(x_{i}^{2}-\mu^{2}\right)-\left(\mu_{M L E}^{2}-\mu^{2}\right)\right]\\ &= \mathbb{E}\left[\frac{1}{N} \sum_{i=1}^{N}\left(x_{i}^{2}-\mu^{2}\right)\right]-\mathbb{E}\left[\left(\mu_{MLE}^{2}-\mu^{2}\right)\right] \\ &= \frac{1}{N} \sum_{i=1}^N \mathbb{E}\left[ x_{i}^2-\mu^2 \right] -\mathbb{E}\left[ \mu_{MLE}^{2}-\mu^{2} \right] \\ &= \frac{1}{N} \sum_{i=1}^N \left(\underbrace{ \mathbb{E}\left[ x_{i}^{2} \right] -\mu^{2}}_{{\color{Green} \text{Var}(x_i)=\sigma ^2} } \right) -\mathbb{E}\left[ \mu_{MLE}^{2}-\mu^{2} \right] \qquad (Var(X)=\mathbb{E}\left[ X^{2} \right]-\mathbb{E}^{2}(X) )\\ &= \sigma^{2} -\mathbb{E}\left[ \mu_{LE}^{2}-\mu^{2} \right] \\ &= \sigma^{2} -\mathbb{E}\left[ \mu_{LE}^{2} \right] -\mathbb{E}\left[ \mu^{2} \right] \\ &= \sigma^{2} -\mathbb{E}\left[ \mu_{LE}^{2} \right] -\mu^{2} \\ &= \sigma^{2} -\underbrace{\mathbb{E}\left[ \mu_{LE}^{2} \right] -\mathbb{E}^{2}\left[ \mu_{MLE} \right] }_{Var\left[ \mu_{MLE} \right] } \\ &=\sigma^{2}-\operatorname{Var}\left[\frac{1}{N} \sum_{i=1}^{N} x_{i}\right]\\ &=\sigma^{2}-\frac{1}{N^{2}} \sum_{i=1}^{N} \operatorname{Var}\left[x_{i}\right] \qquad (Var(CX)=D^{2}Var(X))\\ &=\sigma^{2}-\frac{1}{N^{2}} N \sigma^{2} \\ &=\frac{N-1}{N} \sigma^{2} \end{split}

所以，σMLE2\sigma^{2}_{MLE} 是有偏估计量，而且和真实值比较小，

info

而 σ^2=1N−1∑i=1N(xi−μMLE)2\displaystyle\hat{\sigma}^{2}=\frac{1}{N-1}\sum_{i=1}^N\left( x_{i}-\mu_{MLE} \right)^{2} 是无偏估计。

高维高斯分布​

对于多变量的高斯分布 X∼N(μ,Σ)X\sim \mathcal{N}(\mu,\Sigma)，概率密度函数为：

p(X)=12πp2∣Σ∣12exp⁡{−12(X−μ)TΣ−1(X−μ)}p(X)=\frac{1}{\sqrt{2 \pi}^{\frac{p}{2}}|\Sigma|^{\frac{1}{2}}} \exp \left\{-\frac{1}{2}(X-\mu)^{T} \Sigma^{-1}(X-\mu)\right\}

其中，X∈RpX \in \mathbb{R}^p,

X=(x1x2⋮xp)μ=(μ1μ2⋮μp)Σ=(σ11σ12⋯σ1pσ21σ22⋯σ2p⋮⋮⋱⋮σp1σp2⋯σpp)p×pX=\begin{pmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{p} \end{pmatrix} \quad \mu=\begin{pmatrix} \mu_1 \\ \mu_{2} \\ \vdots \\ \mu_{p} \end{pmatrix} \quad \Sigma=\begin{pmatrix} \sigma_{11} & \sigma_{12} & \cdots & \sigma_{1 p} \\ \sigma_{21} & \sigma_{22} & \cdots & \sigma_{2 p} \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_{p 1} & \sigma_{p 2} & \cdots & \sigma_{p p} \end{pmatrix}_{p \times p}

其中 Σ\Sigma 一般为 半正定矩阵(This page is not published)。

马氏距离​

(X−μ)TΣ−1(X−μ)(X-\mu)^{T} \Sigma^{-1}(X-\mu) 的计算结果是一个数，这个数被称为马氏距离。设我们有两个向量：

z1=(z11,z12)⊤,z2=(z21,z22)⊤z_{1}=(z_{11},z_{12})^\top,z_{2}=(z_{21},z_{22})^\top

那么 z1z_{1} 和 z2z_{2} 之间的马氏距离为：

(z1−z2)TΣ−1(z1−z2)=(z11−z12z21−z22)Σ−1(z11−z12z21−z22)\left(z_{1}-z_{2}\right)^{T} \Sigma^{-1}\left(z_{1}-z_{2}\right)=\left(\begin{array}{ll} z_{11}-z_{12} & z_{21}-z_{22} \end{array}\right) \Sigma^{-1}\begin{pmatrix} z_{11}-z_{12} \\ z_{21}-z_{22} \end{pmatrix}

显然，当 Σ−1=I\Sigma^{-1}=I 时，马氏距离等于欧氏距离 (z1−z2)TΣ−1(z1−z2)=(z11−z12)2+(z21−z22)2\left(z_{1}-z_{2}\right)^{T} \Sigma^{-1}\left(z_{1}-z_{2}\right)=\left(z_{11}-z_{12}\right)^{2}+\left(z_{21}-z_{22}\right)^{2}

这东西是个啥​

这一坨东西表示了啥呢？

由于 Σ\Sigma 是一个实对称矩阵，那么对 Σ\Sigma 进行特征分解，那么有 Σ=UΛU⊤\Sigma=U \Lambda U^{\top }，并且 UU⊤=U⊤U=IUU^\top=U^\top U=I，所以 U−1=U⊤U^{-1}=U^\top，Λ=diag⁡(λi)(i=1,2,⋯ ,N)\Lambda=\operatorname{diag}\left(\lambda_{i}\right) \quad(i=1,2, \cdots, N)，并且 U=(U1,U2,⋯ ,Up)p×pU=\left(U_{1}, U_{2}, \cdots, U_{p}\right)_{p \times p}

Σ=UΛUT=(U1,U2,⋯ ,Up)(λ1λ2⋱λp)(U1TU2T⋮UpT)=(U1λ1,U2λ2,⋯ ,Upλp)(U1TU2T⋮UpT)=∑i=1pUiλiUiT\begin{aligned} \Sigma & =U \Lambda U^{T} \\ & =\left(U_{1}, U_{2}, \cdots, U_{p}\right)\begin{pmatrix} \lambda_{1} & & & \\ & \lambda_{2} & & \\ & & \ddots & \\ & & & \lambda_{p} \end{pmatrix}\begin{pmatrix} U_{1}^{T} \\ U_{2}^{T} \\ \vdots \\ U_{p}^{T} \end{pmatrix} \\ & =\left(U_{1} \lambda_{1}, U_{2} \lambda_{2}, \cdots, U_{p} \lambda_{p}\right)\begin{pmatrix} U_{1}^{T} \\ U_{2}^{T} \\ \vdots \\ U_{p}^{T} \end{pmatrix} \\ & =\sum_{i=1}^{p} U_{i} \lambda_{i} U_{i}^{T} \end{aligned}

而 Σ−1\Sigma^{-1} 是啥勒？

Σ−1=(UΛUT)−1=(UT)−1Λ−1U−1=UΛ−1UT\Sigma^{-1}=\left(U \Lambda U^{T}\right)^{-1}=\left(U^{T}\right)^{-1} \Lambda^{-1} U^{-1}=U \Lambda^{-1} U^{T}
warning

这里的 UU 是正交矩阵，所以 U⊤=U−1U^\top=U^{-1}

而 Λ\Lambda 是一个对角线矩阵，所以

Λ−1=diag(1λi),i=1,⋯ ,p\Lambda^{-1} = diag(\frac{1}{\lambda_{i}}),\quad i=1,\cdots,p

所以：

Σ−1=∑i=1pUi1λiUiT\Sigma^{-1}=\sum_{i=1}^{p} U_{i} \frac{1}{\lambda_{i}} U_{i}^{T}

那么代入到前面的马氏距离公式，

(X−μ)TΣ−1(X−μ)=(X−μ)T∑i=1pUi1λiUiT(X−μ)=∑i=1p(X−μ)TUi1λiUiT(X−μ)\begin{aligned} (X-\mu)^{T} \Sigma^{-1}(X-\mu) & =(X-\mu)^{T} \sum_{i=1}^{p} U_{i} \frac{1}{\lambda_{i}} U_{i}^{T}(X-\mu) \\ & =\sum_{i=1}^{p}(X-\mu)^{T} U_{i} \frac{1}{\lambda_{i}} U_{i}^{T}(X-\mu) \end{aligned}

令 yi=(X−μ)⊤Uiy_{i}=(X-\mu)^\top U_{i}，则上式可以变化为：

(X−μ)TΣ−1(X−μ)=∑i=1pyi1λiyiT=∑i=1pyi2λi(X-\mu)^{T} \Sigma^{-1}(X-\mu) =\sum_{i=1}^{p} y_{i} \frac{1}{\lambda_{i}} y_{i}^{T}=\sum_{i=1}^p \frac{y_{i}^{2}}{\lambda_{i}}
怎么理解呢？

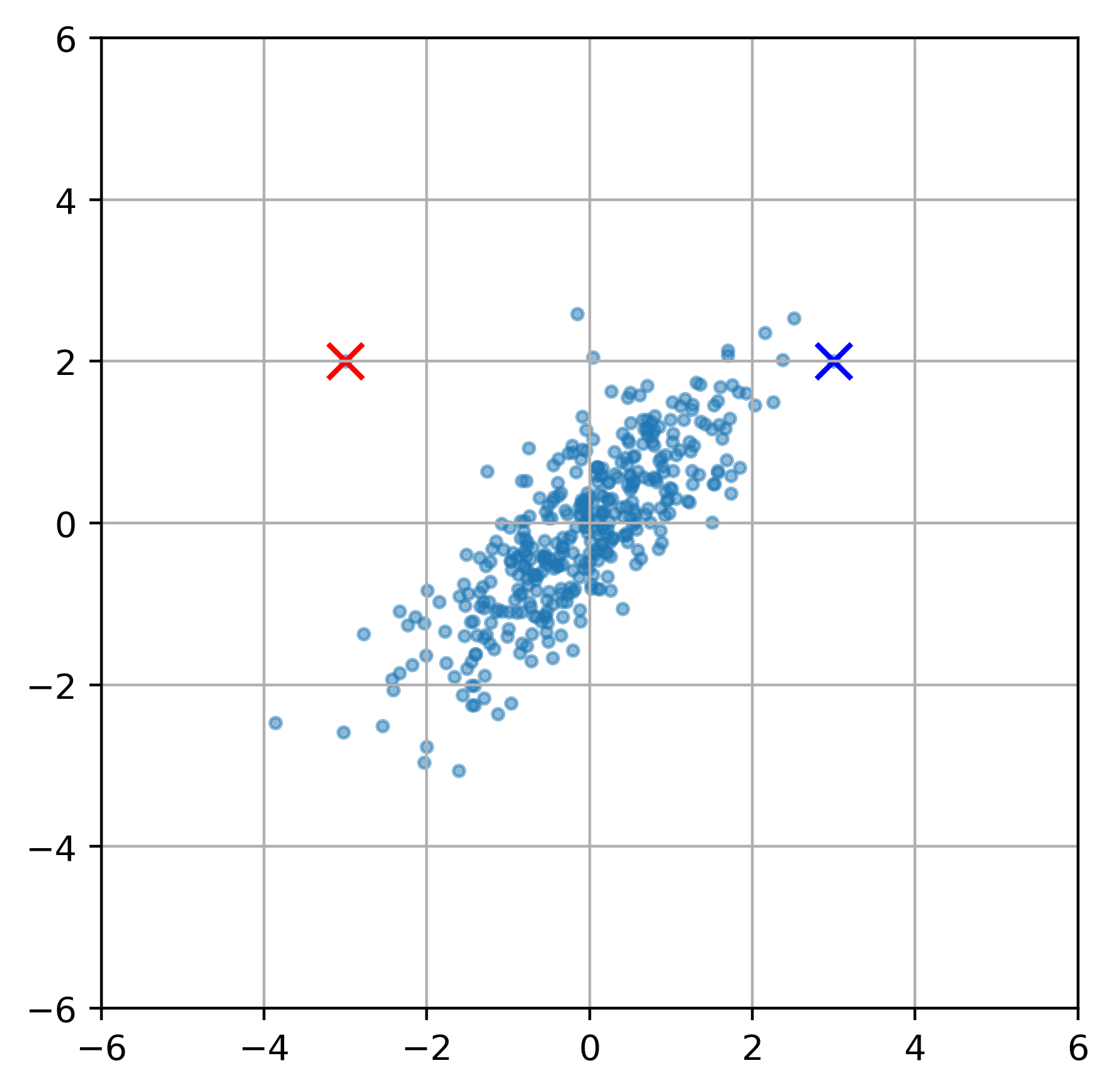
image.png

上图我们有红点和蓝点，他们与整个样本的 " 中心 " 的欧式距离都是一样的，但是马氏距离会怎么样呢？

首先我们先做变换 (X−μ)⊤Ui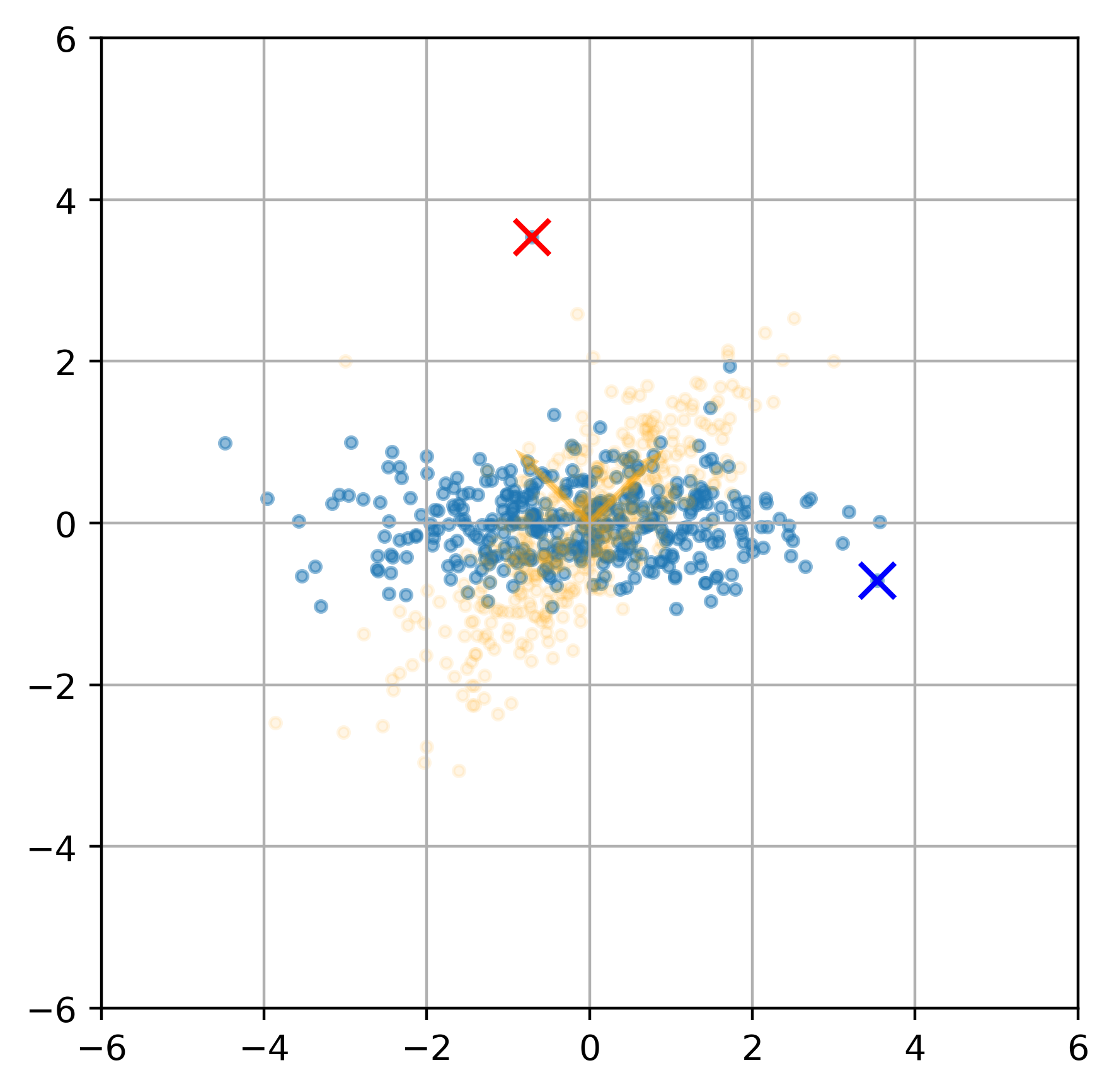\left( X-\mu \right)^\top U_{i} image.png 这个变换就是将样本先平移到原点，然后将原始的特征轴旋转成为主轴 (UU 矩阵是正交矩阵)

而之后 yiλi\displaystyle\frac{y_{i}}{\lambda_{i}} 实际上就是标准化 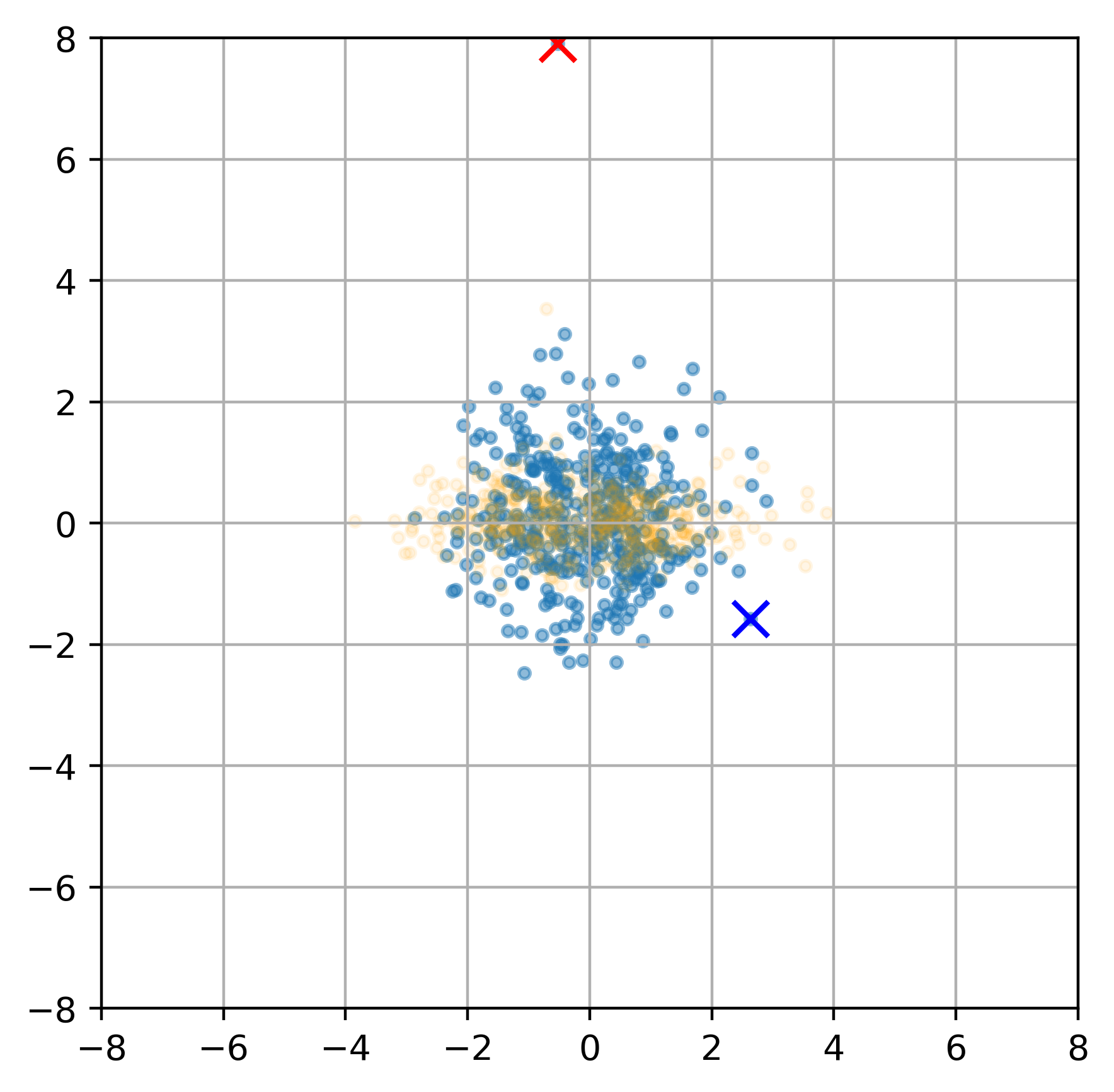image.png 这样计算两个点的欧式距离就可以区分开了。

和 PCA 的关系

有主成分分析可知，主成分实际上就是特征向量的方向，而每个方向的方差就是对应的特征值，所以马氏距离就是 PCA+NormPCA+Norm

note

所以表达式 (X−μ)TΣ−1(X−μ)(X-\mu)^{T} \Sigma^{-1}(X-\mu) 实际上是在描述一个样本对于总体样本 " 中心 " 的距离，而概率密度函数

p(X)=12πp2∣Σ∣12exp⁡{−12(X−μ)TΣ−1(X−μ)}p(X)={\color{Red} \frac{1}{\sqrt{2 \pi}^{\frac{p}{2}}|\Sigma|^{\frac{1}{2}}}} \exp \left\{-\frac{1}{2}(X-\mu)^{T} \Sigma^{-1}(X-\mu)\right\}

前半部分是样本无关的，所以对于一个样本来说其概率与对总体样本 " 中心 " 的马氏距离负相关。

高维问题​

tip

由于 Σ\Sigma 是一个 p×pp \times p 是对称矩阵，所以有 p(p+1)2\displaystyle \frac{p(p+1)}{2} 个参数。一旦输入维度过大，这个矩阵的计算会很复杂。所以有些时候会进行假设

可以假设其是对角矩阵，甚至在各向同性假设中假设其对角线上的元素都相同。前一种就是 Factor Analysis\text{Factor Analysis} 后一种有概率 PCA:Principle Component Analysis(p-PCA)

tip

单个高斯分布是单峰的，对于有多峰的数据分布肯定是不合适的，所以会有 混合高斯模型(GMM)

相关资料​