N 维空间下两个随机向量的夹角

我们将整个 $n$ 维空间看做为半径 $R\to +\infty$ 的球，考虑到夹角具有伸缩不变性，所以考虑 $x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}\le 1$ 和 $x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2} \le R^2$ 是等价的，所以我们就在 $n$ 维单位球里考虑这个问题就行了。

又注意到夹角具有旋转不变性，不妨设其中一个点为 $A(1,0,0, \cdots, 0)$，另一个点为 $B\left(x_{1}, x_{2}, \cdots x_{n}\right)$，其中 $\left \| \left \{ x_{1}, x_{2}, \cdots x_{n} \right \} \right \| =1$

我们将向量 $\mathbf{x}=\{x_{1}, x_{2}, \cdots x_{n}\}$ 转化为超球坐标

$$\begin{cases} x_{1} =\cos \left(\varphi_{1}\right) \\ x_{2} =\sin \left(\varphi_{1}\right) \cos \left(\varphi_{2}\right) \\ x_{3} =\sin \left(\varphi_{1}\right) \sin \left(\varphi_{2}\right) \cos \left(\varphi_{3}\right) \\ \vdots \\ x_{n-1} =\sin \left(\varphi_{1}\right) \cdots \sin \left(\varphi_{n-2}\right) \cos \left(\varphi_{n-1}\right) \\ x_{n} =\sin \left(\varphi_{1}\right) \cdots \sin \left(\varphi_{n-2}\right) \sin \left(\varphi_{n-1}\right) \end{cases}$$

这里最后的一个 $\varphi_{n-1} \in[0,2 \pi)$，其余的 $\varphi\in[0,\pi]$。此时，$A,B$ 的夹角为

$$\cos \Theta=\frac{x_{1}}{\sqrt{x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}}}=\cos(\varphi_{1})$$

也就是说二者的夹角正好为 $\varphi_{1}$，那么，$A,B$ 的夹角 $\Theta$ 不超过 $\theta$ 的概率是：

$$P_{n}\{\Theta \leq \theta \}=\frac{n \text { 维超球面上 } \varphi_{1} \text { 不超过 } \theta \text { 的积分 }}{n \text { 维超球面上的全积分 }}$$

而 $n$ 维超球面上的积分微元是 $\sin ^{n-2}\left(\varphi_{1}\right) \sin ^{n-3}\left(\varphi_{2}\right) \cdots \sin \left(\varphi_{n-2}\right) d \varphi_{1} d \varphi_{2} \cdots d \varphi_{n-1}$，所以

$$\begin{aligned} P_{n}\left(\Theta \leq \theta\right) & = \frac{\int_{0}^{2 \pi} \cdots \int_{0}^{\pi} \int_{0}^{\theta} \sin ^{n-2}\left(\varphi_{1}\right) \sin ^{n-3}\left(\varphi_{2}\right) \cdots \sin \left(\varphi_{n-2}\right) d \varphi_{1} d \varphi_{2} \cdots d \varphi_{n-1}}{\int_{0}^{2 \pi} \cdots \int_{0}^{\pi} \int_{0}^{\pi} \sin ^{n-2}\left(\varphi_{1}\right) \sin ^{n-3}\left(\varphi_{2}\right) \cdots \sin \left(\varphi_{n-2}\right) d \varphi_{1} d \varphi_{2} \cdots d \varphi_{n-1}} \\ & =\frac{(n-1) \text { 维单位超球的表面积 } \times \int_{0}^{\theta} \sin ^{n-2} \varphi_{1} d \varphi_{1}}{n \text { 维单位超球的表面积 }} \\ & =\frac{\Gamma\left(\frac{n}{2}\right)}{\Gamma\left(\frac{n-1}{2}\right) \sqrt{\pi}} \int_{0}^{\theta} \sin ^{n-2} \varphi_{1} d \varphi_{1} \end{aligned}$$

这表明 $\theta$ 的概率密度函数为

$$\begin{aligned} f_{\Theta}(\theta)&=\frac{\mathrm{d}}{\mathrm{d} \theta} P\{\Theta \leqslant \theta\}\\ &=\frac{\Gamma\left(\frac{n}{2}\right) \sin ^{n-2} \theta}{\sqrt{\pi} \Gamma\left(\frac{n-1}{2}\right)} \end{aligned}$$

这个函数长什么样子呢

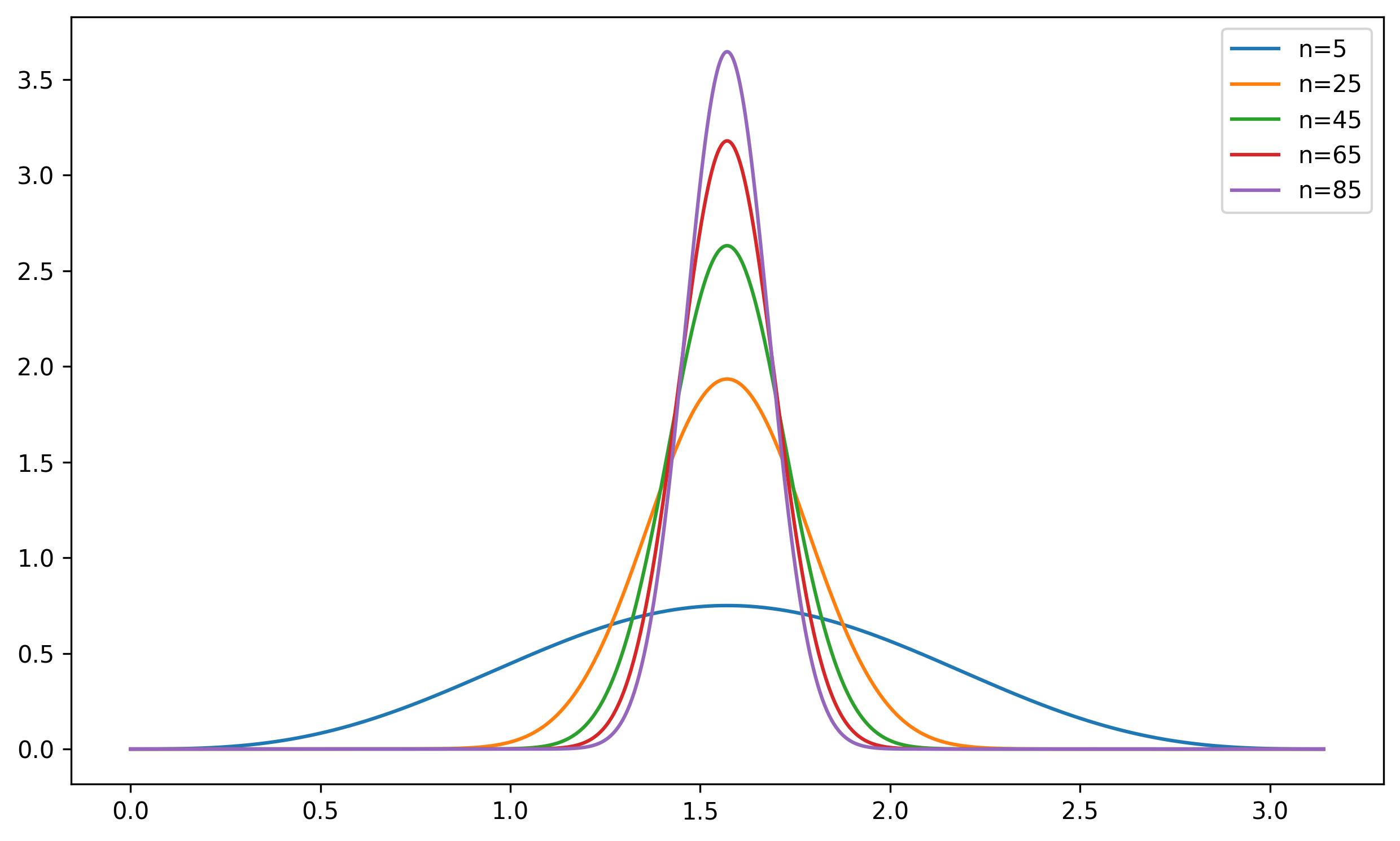
另外如果需要 $\eta=\cos(\theta)$ 的分布，这需要换元得到

$$\begin{aligned} f_{n}(\eta) & =\frac{\Gamma\left(\frac{n}{2}\right)}{\Gamma\left(\frac{n-1}{2}\right) \sqrt{\pi}} \sin ^{n-2}(\arccos \eta)\left|\frac{d \theta}{d \eta}\right| \\ & =\frac{\Gamma\left(\frac{n}{2}\right)}{\Gamma\left(\frac{n-1}{2}\right) \sqrt{\pi}}\left(1-\eta^{2}\right)^{(n-3) / 2} \end{aligned}$$

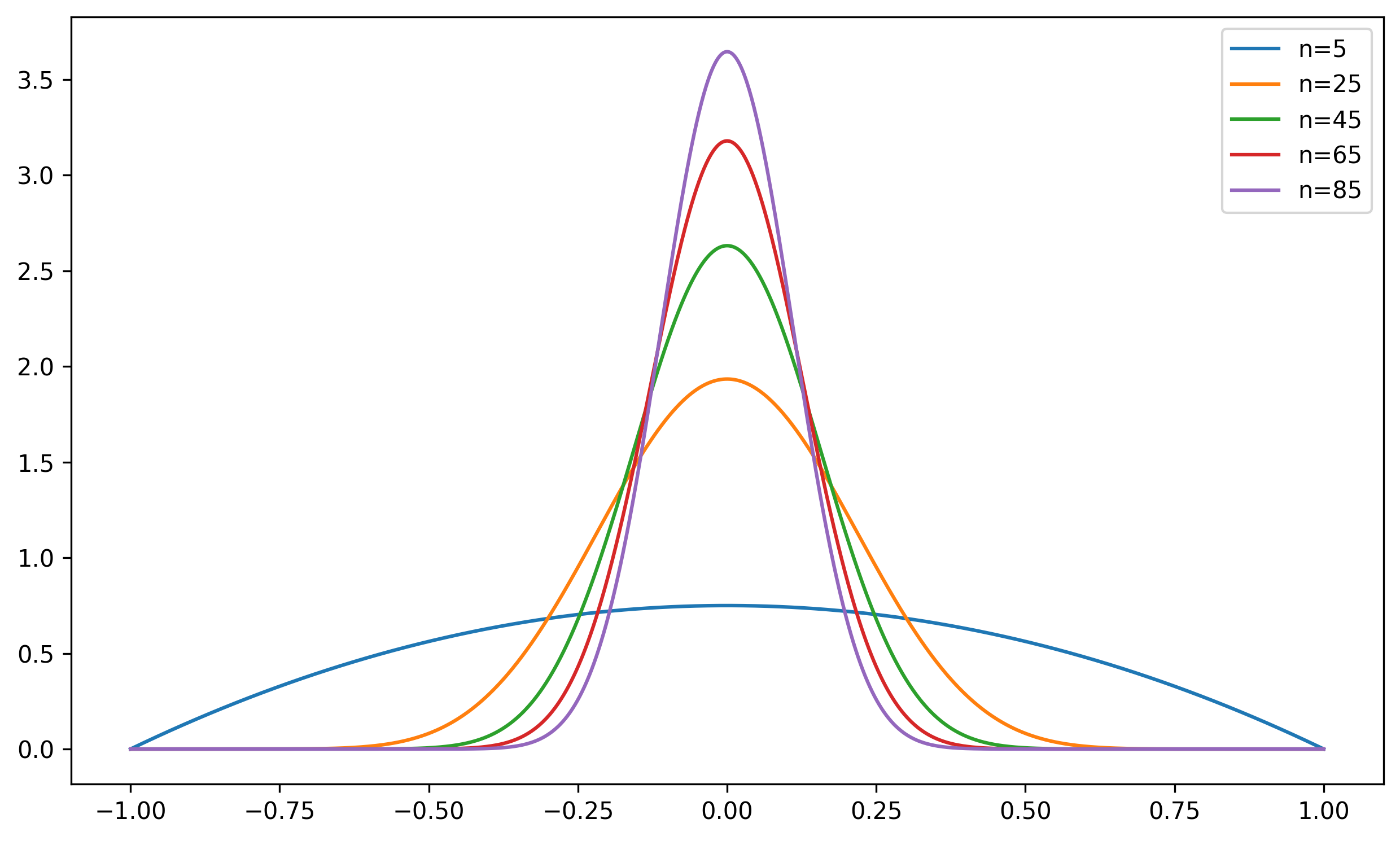
所以可以看到函数在 $\theta=\frac{\pi}{2}$ 取到最大值，并且当 $n\to \infty$ 时，趋向于冲激函数，即：

$$\lim _{n \rightarrow \infty} f_{\Theta}(\theta)=\delta\left(\theta-\frac{\pi}{2}\right)$$

另外我们还要考虑方差

$$\operatorname{Var}_{n}(\theta)=\frac{\Gamma\left(\frac{n}{2}\right)}{\Gamma\left(\frac{n-1}{2}\right) \sqrt{\pi}} \int_{0}^{\pi}\left(\theta-\frac{\pi}{2}\right)^{2} \sin ^{n-2} \theta d \theta$$

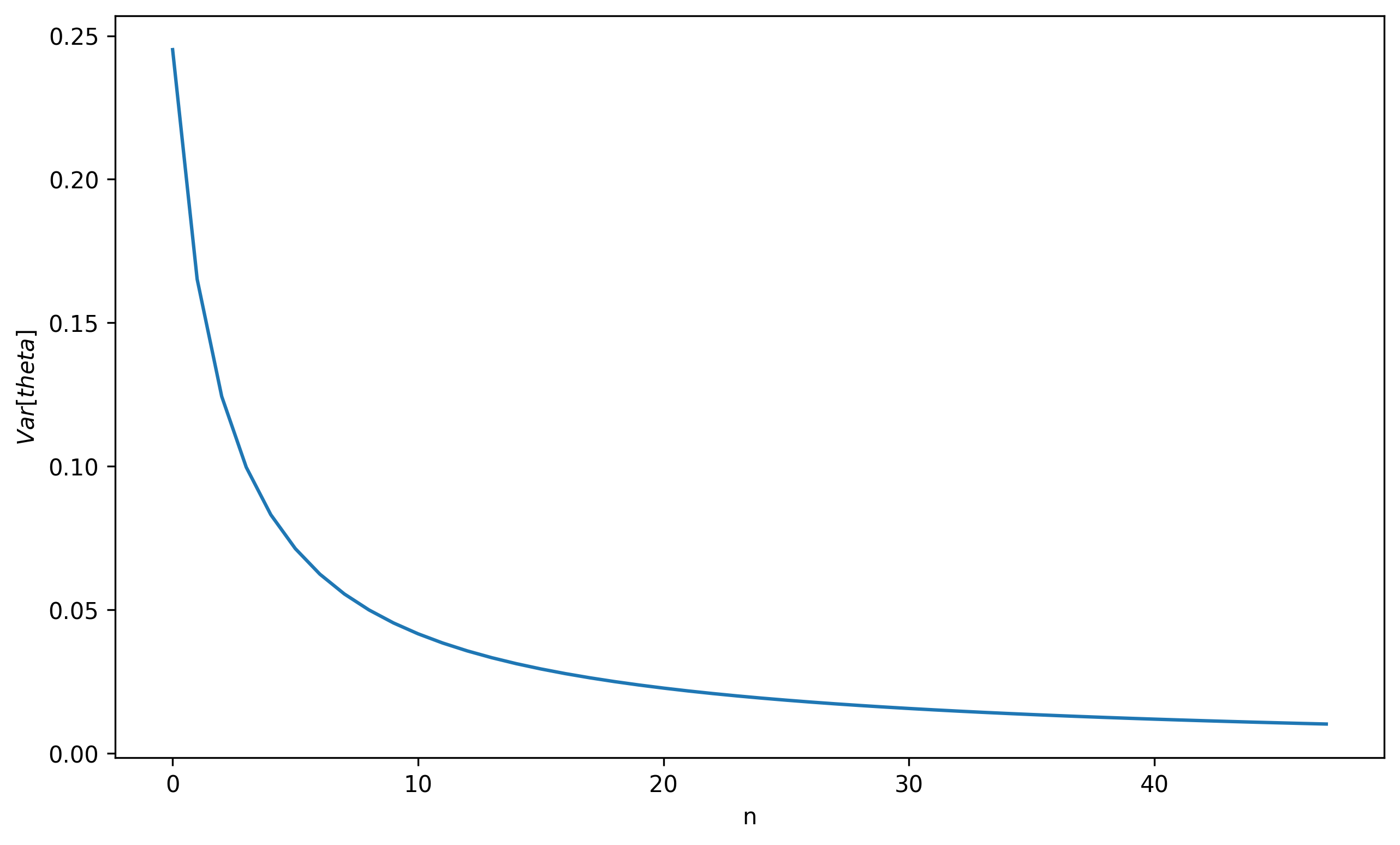
可以看到随着 $n$ 的增大，方差越来越小，这意味着高维空间中的任意两个向量的夹角几乎集中在 $\frac{\pi}{2}$ 附近，换言之，高维空间中任意两个向量几乎都是垂直的。