Skip to main content

机器学习 - 凸优化

· 6 min read
PuQing
PuQing
AI, CVer, Pythoner, Half-stack Developer
定义

凸优化问题 (OPT,convex optimization problem) 指定义在凸集中的凸函数最优化的问题。

数学概念​

凸集​

定义

假设 CC 是向量空间的集。若对于任意 x,y∈Cx,y\in C 和任意的 θ∈R\theta\in \mathbb{R}，满足 0≤θ≤10\le \theta \le 1 时，θx+(1−θ)y∈C\theta x+(1-\theta)y \in C 恒成立。则称 CC 为 凸集1

从几何上来看，就是 CC 中的任意两点之间的直线段都属于 CC。

下面举几个例子：

info

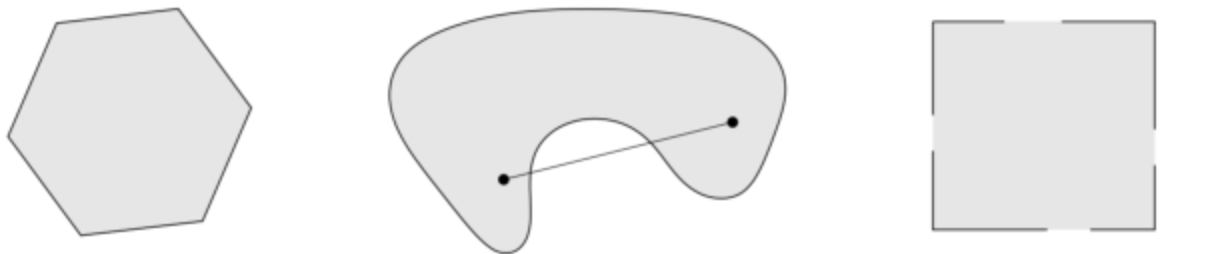
image.png

  1. 是凸集 (集合中的任意两个点连线段中的所有点，都在集合中)
  2. 不是凸集，有空隙
  3. 不是凸集，有些边不在集合中

凸函数​

定义

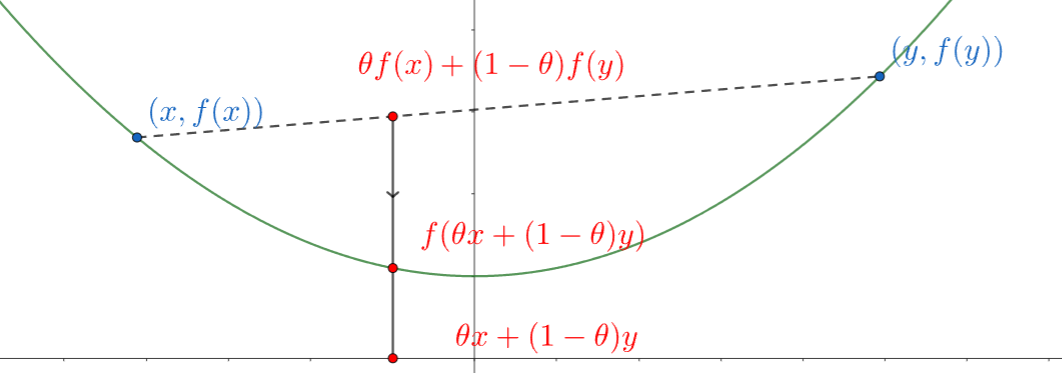
定义在 Rn→R\mathbb{R}^n \to \mathbb{R} 上的函数 ff 是凸函数，如果它的定义域 D(f)\mathbb{D}(f) 是一个凸集且对任意的 x,y∈Dx,y \in \mathbb{D} 和 0≤θ≤1,f(θx+(1−θy))≤θf(x)+(1−θ)f(y)0\le \theta \le 1, f(\theta x+(1-\theta y))\le \theta f(x)+(1-\theta)f(y) 恒成立 2

直观来看：

image.png

info

在函数图形上，任意两点连成的线段，皆位于图形的上方

凸函数的一阶充要条件​

tip

假设定义在 Rn→R\mathbb{R}^n \to \mathbb{R} 上的函数 ff 可微 (对于定义域，梯度 ∇f(x)\nabla f(x) 均存在)。则函数 ff 是凸函数当且仅当函数定义域 D(f)\mathbb{D}(f) 是一个 凸集，且对于所有 x,y∈D(f)x,y\in \mathbb{D}(f) 均满足

f(y)≥f(x)+∇f(x)⊤(y−x)f(y)\ge f(x) + \nabla f(x)^\top(y-x)
info

从几何上来看，即定义域内图形都大于等于该点的切线 (切平面)

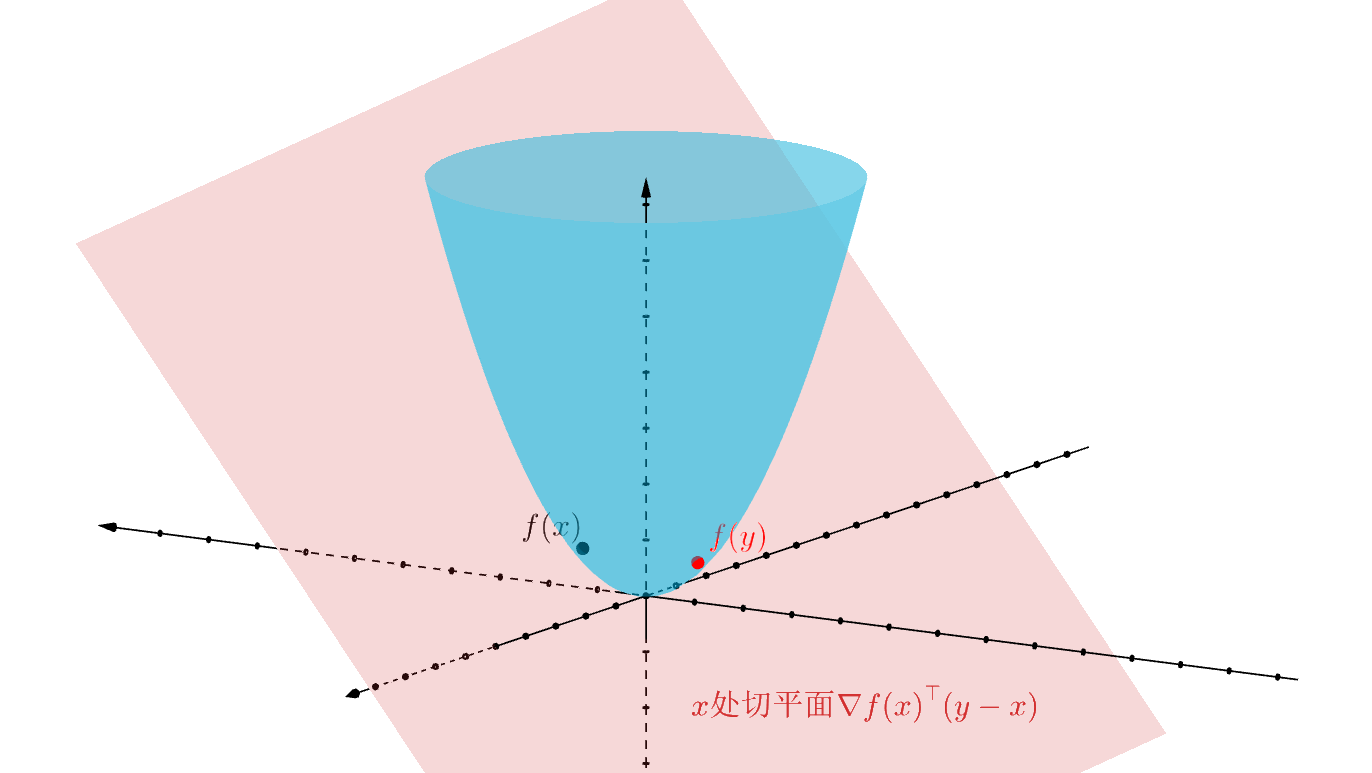
image.png

公式的理解

对于二元函数 f(x,y)f(x,y)

我们知道，函数在某一点 (x0,y0)(x_{0},y_{0}) 处的切平面为

z=fx(x0,y0)(x−x0)+fy(x0,y0)(y−y0)+f(x0,y0)z=f_{x}(x_{0},y_{0})(x-x_{0})+f_{y}(x_{0},y_{0})(y-y_{0}) + f(x_{0},y_{0})

其中的 fx(x0,y0),fy(x0,y0)f_{x}(x_{0},y_{0}),f_{y}(x_{0},y_{0}) 为 ff 在 (x0,y0)(x_{0},y_{0}) 处的偏导数的值，我们可以使用 ∇\nabla 算子 进行表示，并且将自变量视为向量，则：

z=∇f(x0)⊤(x−x0)+f(x0)z = \nabla f(x_{0})^\top(x-x_{0})+f(x_{0})

所以有上面几何理解

凸函数的二阶充要条件​

记函数的一阶导数和二阶导数分别为 gg 和 HH：

g=∇f=[∂f∂x1∂f∂x2⋮∂f∂xn]H=∇2f=[∂2f∂x12∂2f∂x1∂x2⋯∂2f∂x1∂xn∂2f∂x2∂x1∂2f∂x22⋯∂2f∂x2∂xn⋮⋮⋱⋮∂2f∂xn∂x1∂2f∂xn∂x2⋯∂2f∂xn2]g=\nabla f=\left[\begin{array}{c} \frac{\partial f}{\partial x_{1}} \\ \frac{\partial f}{\partial x_{2}} \\ \vdots \\ \frac{\partial f}{\partial x_{n}} \end{array}\right] \quad H=\nabla^{2} f=\left[\begin{array}{cccc} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{1} \partial x_{n}} \\ \frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{2} \partial x_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2} f}{\partial x_{n} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{n} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{n}^{2}} \end{array}\right]

假设定义在 Rn→R\mathbb{R}^n \to \mathbb{R} 上的函数 ff 二阶可微（即海赛矩阵 ∇2f(x)\nabla^2f(x) 存在）。则函数 ff 是凸函数当且仅当函数定义域 D(f)\mathbb{D}(f) 是一个凸集，且对于所有 x∈D(f)x \in \mathbb{D}(f) 均满足：

∇2f(x)⪰0\nabla^2f(x)\succeq 0
info

这里的 ⪰0\succeq 0 表示是半正定的

见 正定矩阵(This page is not published)

凸优化问题​

定义
min⁡f(x)s.t.gi(x)≤0,i=1,2,…,mhj(x)=0,j=1,2,…,n\begin{array}{cl} \min & f(x) \\ s . t . & g_{i}(x) \leq 0, i=1,2, \ldots, m \\ & h_{j}(x)=0, j=1,2, \ldots, n \end{array}

当 f(x)f(x) 和 gi(x)g_{i}(x) 均为凸函数，而 hj(x)h_{j}(x) 均为 仿射变换与仿射函数 时，上述的优化问题即凸优化问题

常见的凸优化问题​

线性规划（LP，Linear Program）
min⁡cTx+d s.t. G(x)⪯hA(x)=b\begin{array}{cl} \min & c^{T} x+d \\ \text { s.t. } & G(x) \preceq h \\ & A(x)=b \end{array}

其中的目标函数和不等式约束都是仿射函数，且 ⪯\preceq 表示按元素小于等于

二次规划（QP，Quadratic Program）
min⁡12xTPx+cTx+d s.t. G(x)⪯hA(x)=b\begin{array}{ll} \min & \frac{1}{2} x^{T} P x+c^{T} x+d \\ \text { s.t. } & G(x) \preceq h \\ & A(x)=b \end{array}

其中目标函数为凸二次型，不等式约束为仿射函数

利用 Python 进行凸优化​

下面是几段例程

给定一个普通的线性规划问题

min⁡z=2x1+3x2+x3{x1+4x2+2x3≥83x1+2x2≥6x1,x2,x3≥0\begin{array}{c} \min z=2 x_{1}+3 x_{2}+x_{3} \\ \left\{\begin{array}{l} x_{1}+4 x_{2}+2 x_{3} \geq 8 \\ 3 x_{1}+2 x_{2} \geq 6 \\ x_{1}, x_{2}, x_{3} \geq 0 \end{array}\right. \end{array} 
import numpy as np

z = np.array([2, 3, 1])

a = np.array([[1, 4, 2], [3, 2, 0]])

b = np.array([8, 6])

x1_bound = x2_bound = x3_bound =(0, None)

from scipy import optimize

res = optimize.linprog(z, A_ub=-a, b_ub=-b,bounds=(x1_bound, x2_bound, x3_bound))

print(res)

#output:
#     fun: 7.0
# message: 'Optimization terminated successfully.'
#     nit: 2
#   slack: array([0., 0.])
#  status: 0
# success: True
#       x: array([0.8, 1.8, 0. ])

参考资料​

Footnotes​

  1. 凸集 - 维基百科，自由的百科全书 ↩

  2. 凸函数 - 维基百科，自由的百科全书 ↩