Nabla 算子与 Laplace 算子

Nabla 算子

Nabla 算子被定义为:

$$\begin{equation} \nabla = \left(\frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z}\right) = \vec{e}_{x} \frac{\partial}{\partial x}+\vec{e}_{y} \frac{\partial}{\partial y}+\vec{e}_{z} \frac{\partial}{\partial z} = \sum_{i = 1}^{3} \vec{e}_{i} \frac{\partial}{\partial x_{i}} \end{equation}$$

$\nabla$ 作用于不同类型的量，得到的就是不同类型的新量：

info

$\nabla$ 直接作用于函数 $F(r)$(不论 $F$ 是标量还是向量），意味着求 $F(r)$ 的 梯度，表示为：$\nabla F(r)$（标量函数的梯度为向量，向量的梯度为二阶张量）；

$\nabla$ 与非标量函数 $F(r)$ 由点积符号 $\cdot$ 连接，意味着求 $F(r)$ 的 散度，表示为：$\nabla \cdot F(r)$；

$\nabla$ 与非标量（三维）函数 $F(r)$ 由叉积符号 $\times$ 连接，意味着求 $F(x)$ 的 旋度，表示为：$\nabla \times F(r)$。

梯度

$\nabla f$ 在三维直角坐标系中表示为：

$$\nabla f=\left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}\right)=\frac{\partial f}{\partial x} \mathbf{i}+\frac{\partial f}{\partial y} \mathbf{j}+\frac{\partial f}{\partial z} \mathbf{k}$$

具体的： 函数 $f(x, y, z)=2 x+3 y^{2}-\sin (z)$ 的梯度为

$$\nabla f=(2,6 y,-\cos (z))=2 \mathbf{i}+6 y \mathbf{j}-\cos (z) \mathbf{k}$$

下面是一个可视化的 Python ：

import numpy as np
import matplotlib.pyplot as plt
import sympy as sp
x, y = sp.symbols("x y")

func = sp.sin(x) + sp.cos(y)
nabla = sp.Matrix([sp.diff(func, x), sp.diff(func, y)])
x_range = np.linspace(-np.pi, np.pi, 100)
y_range = np.linspace(-np.pi, np.pi, 100)
X, Y = np.meshgrid(x_range, y_range)
Z = sp.lambdify((x, y), func, "numpy")(X, Y)
nable_points = sp.lambdify((x, y), nabla, "numpy")(X, Y).reshape(2, 100, 100)
fig = plt.figure(figsize=(8, 8), dpi=200)
ax = fig.add_subplot(111)
ax.pcolormesh(X, Y, Z, cmap="jet")
ax.streamplot(X, Y, nable_points[0], nable_points[1], color="k")
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_title("f(x, y) = sin(x) + cos(y)")
plt.show()

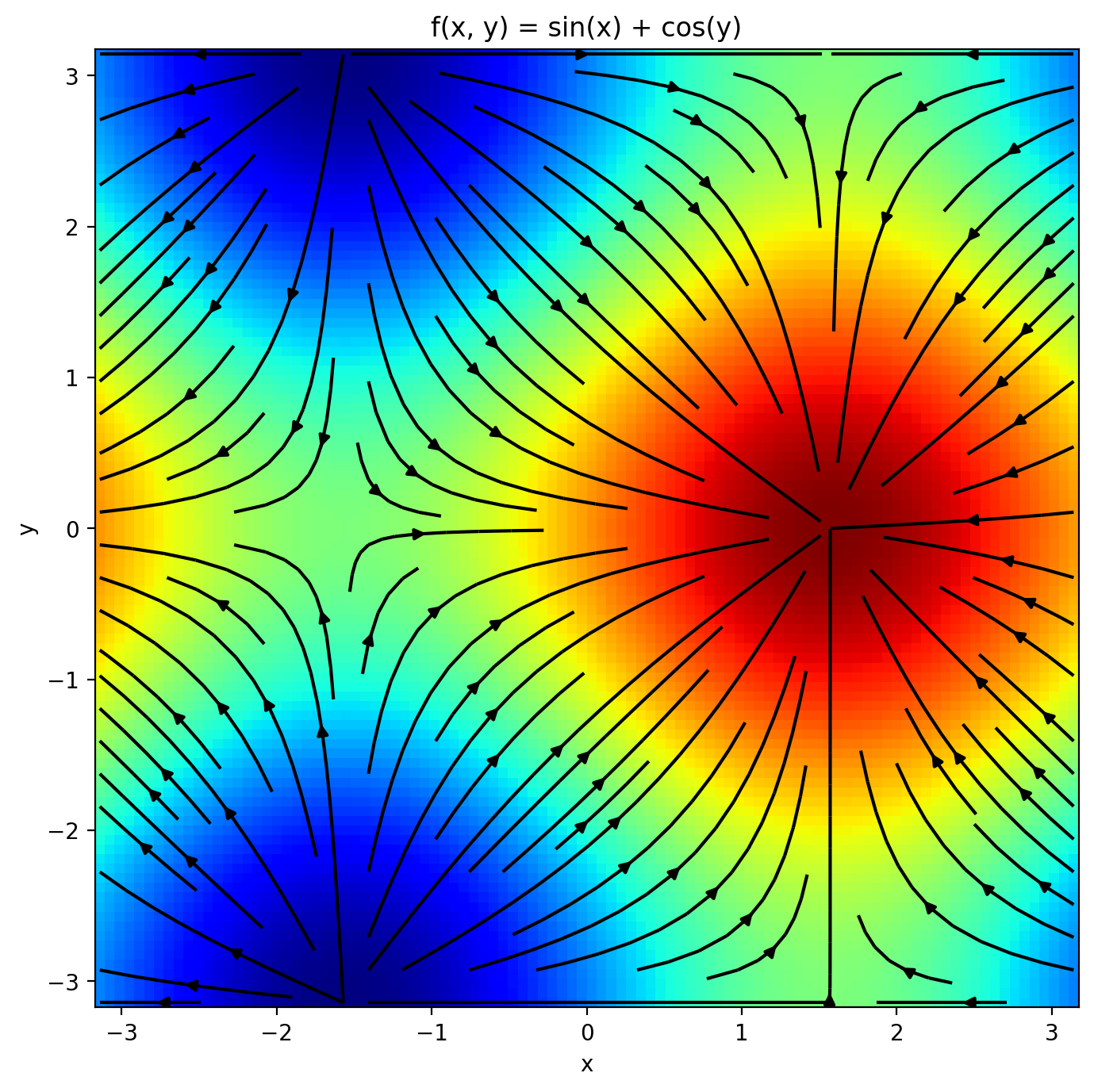
它将每个标量场变化为了向量场。

散度

在三维直角坐标系 $x y z$ 中，设向量场 $\mathbf{A}$ 的表示为:

$$\mathbf{A}(x, y, z)=A_{x}(x, y, z) \mathbf{i}+A_{y}(x, y, z) \mathbf{j}+A_{z}(x, y, z) \mathbf{k},$$

其中的 $\mathbf{i}, \mathbf{j}, \mathbf{k}$ 分别是 $x$ 轴、 $y$ 轴、 $z$ 轴方向上的单位向量，场的分量 $A_{x}$, $A_{y}$, $A_{z}$ 具有一阶连续偏导数，那么向量场 $\mathbf{A}$ 的散度就是:

$$\operatorname{div} \mathbf{A}=\nabla \cdot \mathbf{A}=\frac{\partial A_{x}}{\partial x}+\frac{\partial A_{y}}{\partial y}+\frac{\partial A_{z}}{\partial z}$$

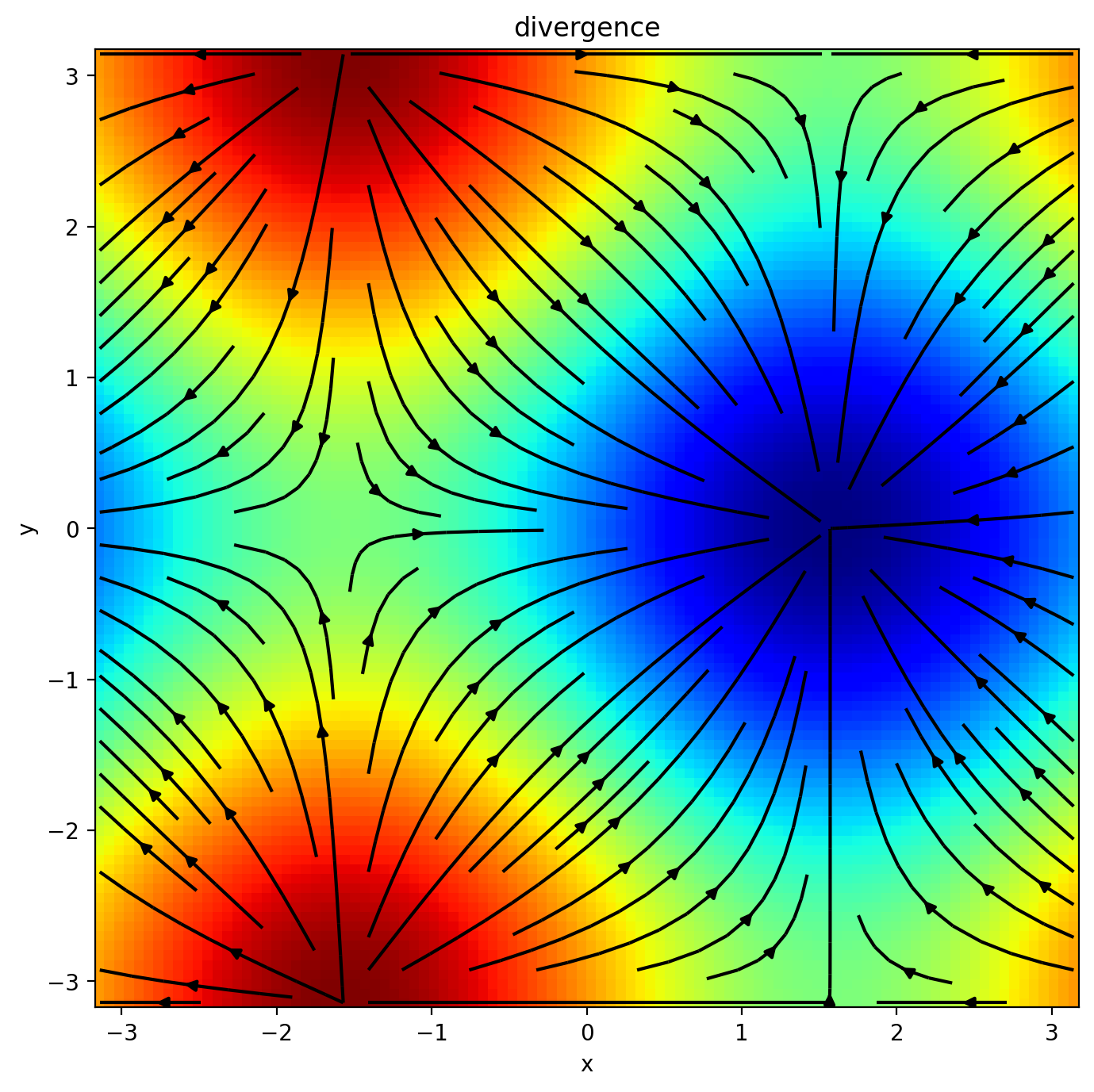而对于向量场使用 $\nabla$ 会将向量场转化为标量场。

Laplace 算子

记 $\Delta=\nabla \cdot \nabla=\displaystyle\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}+\frac{\partial^{2}}{\partial z^{2}}$，称为 Laplace 算子，而满足Laplace方程的函数：

$$\Delta u=\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}}+\frac{\partial^{2} u}{\partial z^{2}}=0$$

称为调和函数。