MCMC

马尔科夫链

在 马尔科夫及其有关的随机过程 中我们介绍过马尔科夫过程，其区别就是时间是否是离散的。整体分类可以见下面表格。

	可数或有限的状态空间	连续或一般的状态空间
离散时间	在可数且有限状态空间下的马尔可夫链	Harris chain (在一般状态空间下的马尔可夫链)
连续时间	Continuous-time Markov process	任何具备马尔可夫性质的连续随机过程，例如维纳过程

马尔可夫链假设某一时刻状态转移的概率只依赖于它的前一个状态。

$$\begin{aligned} & P\left(X_{t+1}=j \mid X_{0}=k_{0}, \ldots X_{t-1}=k_{t-1}, X_{t}=i\right) \\ = & P\left(X_{t+1}=j \mid X_{t}=i\right)=p_{i j}, t=0,1, \ldots, k_{0}, \ldots, k_{t-1}, i, j \in S \end{aligned}$$

则矩阵 $P=(p_{ij})_{m\times m}$ 为转移概率矩阵。显然有 $\sum_{j=1}^{m}p_{ij}=1,i=1,2,\dots,m$。

info

如果我们给定状态空间为 $\{s_{0},s_{1},s_{2}\}$ 三种状态。并给定有转移概率矩阵：

$$P = \begin{bmatrix} 0.6 & 0.2 & 0.2 \\ 0.3 & 0.4 & 0.3 \\ 0 & 0.3 & 0.7 \end{bmatrix}$$

假设初始状态分别为 $\left[ 0.1,0.2,0.7 \right]$ 。我们模拟一下直到 $t=100$ 时状态概率。

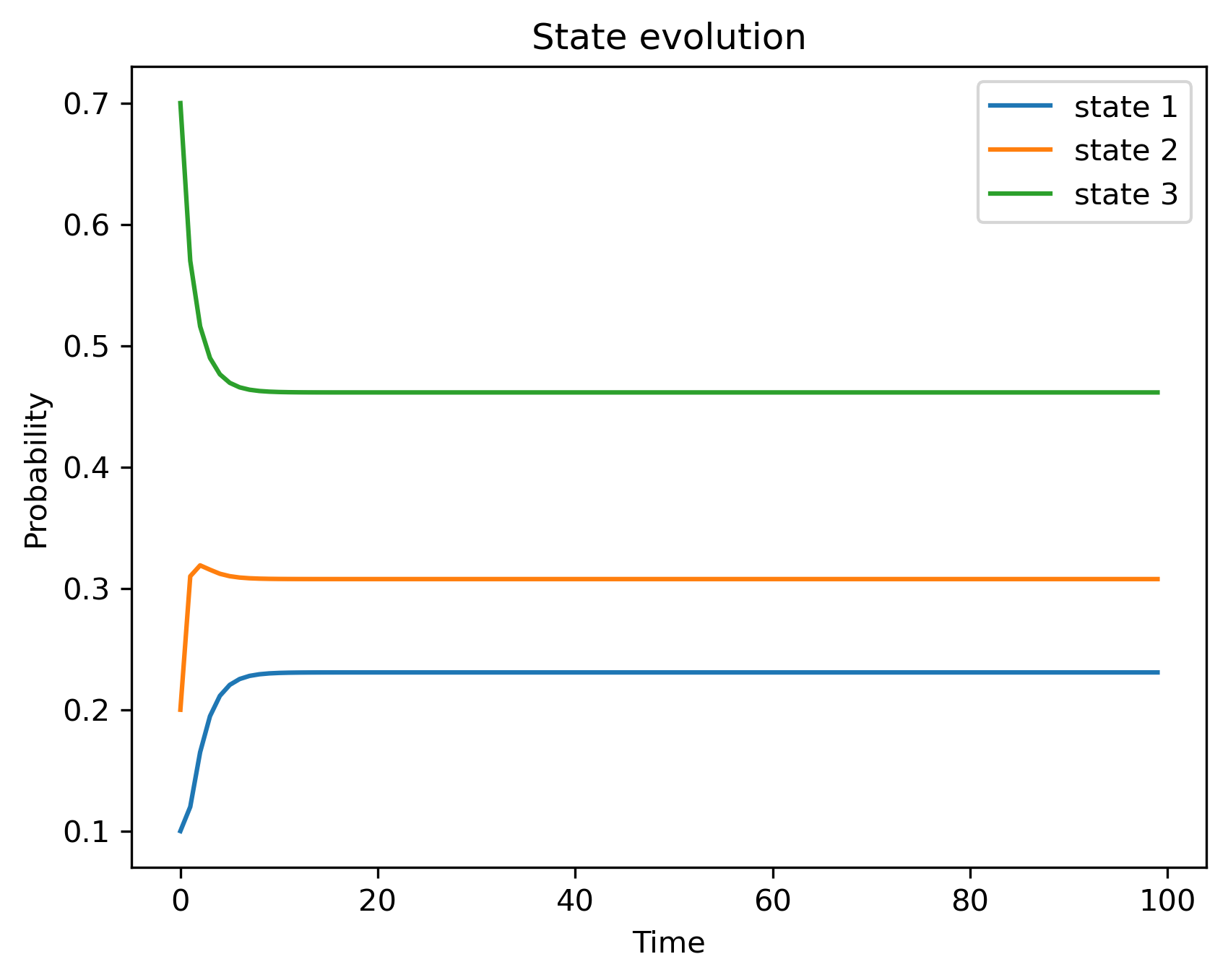可以看到最后的状态概率收敛到一个固定值，我们尝试进行多次，初始不同的状态概率。

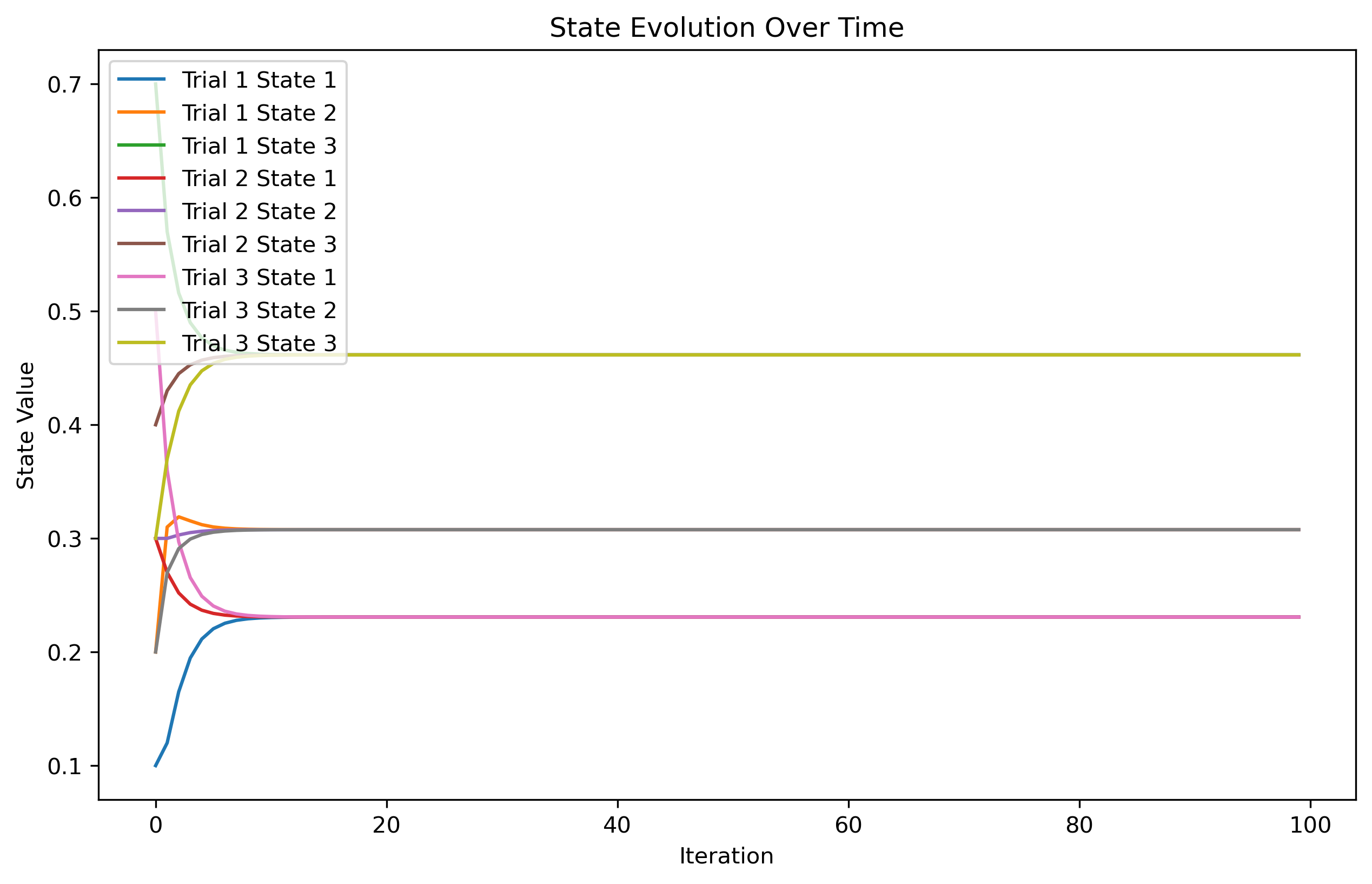
可以看到同样收敛到了一个固定值。

也就是说马尔科夫链模型的状态转移矩阵收敛到的稳定概率分布与初始状态概率分布无关。也就是说，如果我们得到了这个稳定概率分布对应的马尔科夫链模型的状态转移矩阵，则我们可以用任意的概率分布样本开始，带入马尔科夫链模型的状态转移矩阵，这样经过一些序列的转换，最终就可以得到符合对应稳定概率分布的样本。

用数学语言来描述就是

如果一个非周期的马尔科夫有状态转移矩阵 $P$，并且他的任何两个状态是连通的，那么 $\lim _{n \rightarrow \infty} P_{i j}^{n}$ 与初始点 $i$ 无关。我们有

tip

$$\lim _{n \to \infty} P_{i j}^{n}=\pi(j)$$

对于马式链 $P\left(X_{t+k}=j \mid X_{t}=i\right)=p_{i j}^{(k)}$，为 $k$ 步转移概率

tip

$$\lim _{n \to \infty} P^{n}= \begin{bmatrix} \pi(1) & \pi(2) & \cdots & \pi(j) & \cdots \\ \pi(1) & \pi(2) & \cdots & \pi(j) & \cdots \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \pi(1) & \pi(2) & \cdots & \pi(j) & \cdots \\ \vdots & \vdots & \vdots & \ddots & \vdots \end{bmatrix}$$

tip

$$\pi(j)=\sum_{i=0}^{m} \pi(i) P_{i j}$$

证明

$$P\left(X_{n+1}=j\right)=\sum_{i=0}^{\infty} P\left(X_{n}=i\right) P\left(X_{n+1}=j \mid X_{n}=i\right)=\sum_{i=0}^{\infty} P\left(X_{n}=i\right) P_{i j}$$

然后两边取极限，实际上就是在描述极限状况下，任意状态的概率为所有概率转换到该状态的概率和

tip

$\pi$ 是 $\pi P=\pi$ 唯一非负解，$\pi=[\pi(1), \pi(2), \cdots, \pi(j), \cdots]$，并且有 $\sum_{i=1}^{\infty}\pi(i)=1$，$\pi$ 被称为马氏链的平稳分布。

马尔科夫链采样

如果我们知道转移概率矩阵，则我们可以非常方便的采样得到平稳分布的样本集。

1. 输入马尔科夫链状态转移矩阵 $P$，
2. 从任意分布中采样初始状态 $x_{0}$
3. 根据条件概率 $P(x\mid x_{t})$ 采样得到 $P(x_{t+1})$

当 $t$ 很大时，$x_{t}$ 的分布就近似服从 $\pi$，抛弃开始的一段后的 $x_{t}$ 序列就可以做为分布 $\pi$ 的相关的样本，抛弃的一段序列叫做老化期。

均匀分布，Box-Muller 变换

在说 MCMC 采样前，先引入一些前置知识。

均匀分布是很容易采样的，比如在计算机中生成 $[0,1]$ 之间的伪随机数序列，就可以看成是一种均匀分布。而我们常见的概率分布，无论是连续的还是离散的分布，都可以基于 $\mathrm{Uniform}(0,1)$ 的样本生成。例如正态分布可以通过著名的 Box−Muller 变换得到:

Box-Muller 变换

如果随机变量 $U_{1},U_{2}$，独立且 $U_{1},U_{2} \sim \mathbf{U}(0,1)$

$$\begin{array}{l} Z_{0}=\sqrt{-2 \ln U_{1}} \cos \left(2 \pi U_{2}\right) \\ Z_{1}=\sqrt{-2 \ln U_{1}} \sin \left(2 \pi U_{2}\right) \end{array}$$

则 $Z_{0},Z_{1}$ 独立且服从标准正态分布。

其他的连续分布也可以通过一个均匀分布变换得到相应的分布，见 逆变换采样。

拒绝接受采样（Acceptance-Rejection Sampling）

上面采样看上去一片岁月静好的样子，但是如果我们需要对下面概率密度函数对应分布进行采样

$$f(x)= \frac{(x-0.4)^{4}}{\displaystyle \int_{0}^{1}(x-0.4)^{4} d x}$$

这个时候上面两种采样方式均无法进行采样。这个时候引入拒绝接受采样。

info

我们首先需要一个建议分布 (proposal distribution)$G$(并且是已知概率密度函数 $g(x)$) 来产生候选样本。比如均匀分布、正态分布

然后还需要一个辅助的均匀分布 $\mathbf{U}(0,1)$ 估算一个常值 $c$。-- 满足不等式 $c * g(x)\ge f(x)$ 的最小值 $c$

开始样本生成

• 从建议分布 $G$ 采样，得到样本 $Y$
• 从分布 $\mathbf{U(0,1)}$ 采样，得到样本 $U$
• 如果 $U\le \displaystyle \frac{f(Y)}{c*g(Y)}$，则令 $X=Y$(接受 Y 作为采样样本)，否则重新开始

note

如何理解上述采样过程呢？

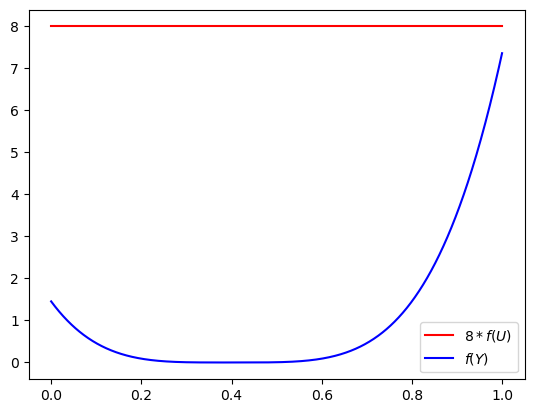
可以看图，上方红色的就是 $c*g(Y)$，蓝色的就是目标概率函数 $f(Y)$。考查下面比值：

$$0< \frac{f(Y)}{c*g(Y)} <1$$

所以我们使用一个辅助的随机变量，如果该随机变量采样使得：

$$U \le \frac{f(Y)}{c*g(Y)}$$

即，该采样落在了 $\frac{f(Y)}{c*g(Y)}$ 的下方，我们就认为该采样值是目标分布 " 采样得到 "，因为接受的概率与拒绝的概率对应着概率密度函数的比值。

细致平稳条件 (Detailed Balance Condition)

再引入细致平稳条件。

如果非周期马尔科夫链状态转移矩阵 $P$ 和概率分布 $\pi(x)$ 对所有的 $i,j$ 满足：

$$\pi(i) P(i, j)=\pi(j) P(j, i), \quad \text { for all } i, j$$

那么 $\pi(x)$ 就是转移概率矩阵的平稳分布。

这也很容易证明。

证明

$$\begin{array}{c} \displaystyle \sum_{i=1}^{\infty} \pi(i) P_{i j}=\sum_{i=1}^{\infty} \pi(j) P_{j i}=\pi(j) \sum_{i=1}^{\infty} P_{j i}=\pi(j) \\ \Rightarrow \pi P=\pi \end{array}$$

当然该条件是一个充分不必要条件。

MCMC 采样

终于可以说 MCMC 采样了，回顾均匀采样、逆变换采样、拒绝接受采样，他们是没有 " 历史信息的 "，所以他们效率非常低。而马氏链这一特性，造就了 MCMC 采样的高效性，采样是一个条件概率采样。

还是同样的问题，对于一个非常复杂的，不可求反函数的高维概率密度函数 $\pi(x)$ 如何采样。

前面我们已经说了对于马氏链来说平稳分布与初始状态分布是无关的，这也就启发我们同样可以采用某种 "proposal distribution"$G$ 然后在 $G$ 上采样然后转换概率矩阵得到平稳分布 $\pi(x)$ 的采样。

但是问题就是如何构造转换概率矩阵？要知道，对于给定的平稳分布 $\pi(x)$ 和某一个马尔可夫状态转移矩阵 $Q$ 不满足细致平稳条件。即：

$$\pi(i) Q(i, j) \neq \pi(j) Q(j, i)$$

其中的 $Q(i,j)$ 还可以表示为 $Q(i, j) \Leftrightarrow Q(j \mid i) \Leftrightarrow Q(i \rightarrow j)$，表示 $i$ 向 $j$ 转移的概率。

但是有意思的来了，虽然 $a \ne b$，但是 $ab=ba$(废话)。同样的构造，我们令 $a(i,j)=\pi(j)Q(j,i)$，我们就有

$$\pi(i) \underbrace{Q(i, j) \alpha(i, j)}_{\hat{Q}(i,j)} =\pi(j) \underbrace{Q(j, i) \alpha(j, i)}_{\hat{Q}(j,i)}$$

而这个新的状态转移矩阵正好满足了细致平稳条件，而平稳分布 $\pi(i)$ 就是在新的 $\hat{Q}$ 下的平稳分布，我们不妨把原始 $Q$ 的平稳分布记做 $\hat{\pi}$。而这恰好构成了拒绝接受采样的两组概率分布。

其中的 $\hat{\pi}$ 是我们容易得到的，因为其转换概率矩阵 $Q$ 已知。

所以我们就有 MCMC 采样方法：

• 从任意简单概率分布采样得到 $x_{0}$
• 从条件概率分布 $Q(x\mid x_{t})$ 得到 $x^*$(类似于拒绝接受采样中的已知概率密度函数的采样)
• 从均匀分布中采样 $U\sim \mathbf{U}(0,1)$
• 如果 $U< a(x_{t},x_{*})=\pi(x_{*})Q(x_{*},x_{t})$，则接受 $x_{t}\to x_{*}$，即 $x_{t+1}=x_{*}$

这里的 $U< a(x_{t},x_{*})$ 是如何得到的？

我们在拒绝接受采样中知道；这实际上目标概率密度与已知概率密度的比值

$$\frac{\pi(x_{*})}{\hat{\pi}(x_{*})} = \frac{\pi(x_{t})\hat{Q}}{\pi(x_{t})Q} = a(x_{t},x_{*})$$

参考

• zhuanlan.zhihu.com/p/37121528
• 【搜出来的文本】⋅（二）从MCMC到模拟退火 - 科学空间|Scientific Spaces